Question Number 178400 by infinityaction last updated on 16/Oct/22
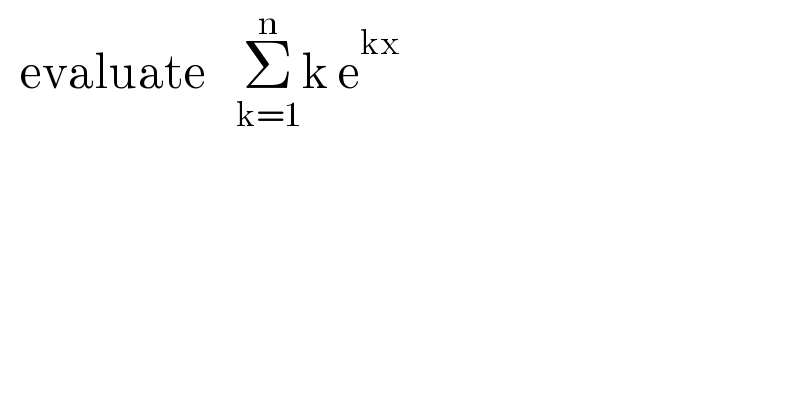
$$\:\:\mathrm{evaluate}\:\:\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{k}\:\mathrm{e}^{\mathrm{kx}} \\ $$
Answered by mr W last updated on 16/Oct/22
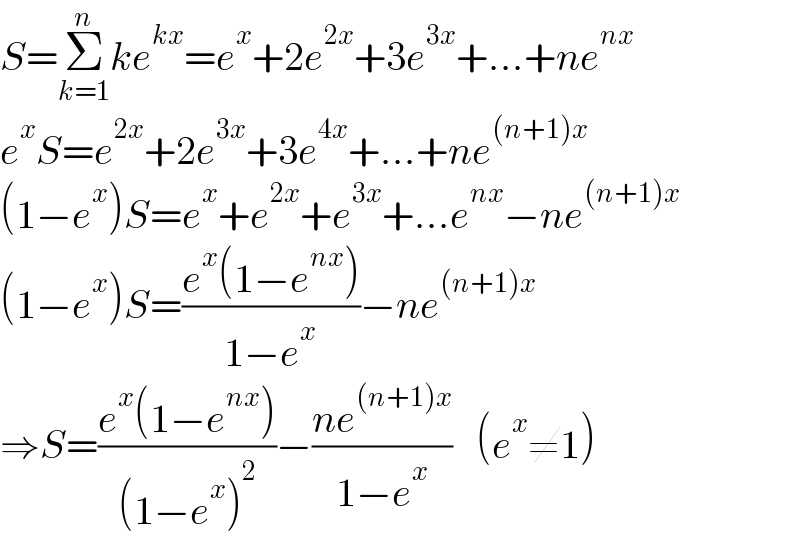
$${S}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{ke}^{{kx}} ={e}^{{x}} +\mathrm{2}{e}^{\mathrm{2}{x}} +\mathrm{3}{e}^{\mathrm{3}{x}} +…+{ne}^{{nx}} \\ $$$${e}^{{x}} {S}={e}^{\mathrm{2}{x}} +\mathrm{2}{e}^{\mathrm{3}{x}} +\mathrm{3}{e}^{\mathrm{4}{x}} +…+{ne}^{\left({n}+\mathrm{1}\right){x}} \\ $$$$\left(\mathrm{1}−{e}^{{x}} \right){S}={e}^{{x}} +{e}^{\mathrm{2}{x}} +{e}^{\mathrm{3}{x}} +…{e}^{{nx}} −{ne}^{\left({n}+\mathrm{1}\right){x}} \\ $$$$\left(\mathrm{1}−{e}^{{x}} \right){S}=\frac{{e}^{{x}} \left(\mathrm{1}−{e}^{{nx}} \right)}{\mathrm{1}−{e}^{{x}} }−{ne}^{\left({n}+\mathrm{1}\right){x}} \\ $$$$\Rightarrow{S}=\frac{{e}^{{x}} \left(\mathrm{1}−{e}^{{nx}} \right)}{\left(\mathrm{1}−{e}^{{x}} \right)^{\mathrm{2}} }−\frac{{ne}^{\left({n}+\mathrm{1}\right){x}} }{\mathrm{1}−{e}^{{x}} }\:\:\:\left({e}^{{x}} \neq\mathrm{1}\right) \\ $$
Commented by infinityaction last updated on 16/Oct/22

$${thanks}\:{sir} \\ $$
Commented by haladu last updated on 16/Oct/22

$$\boldsymbol{\mathrm{Nice}}!\:\boldsymbol{\mathrm{solution}} \\ $$
