Question Number 100215 by Rio Michael last updated on 25/Jun/20
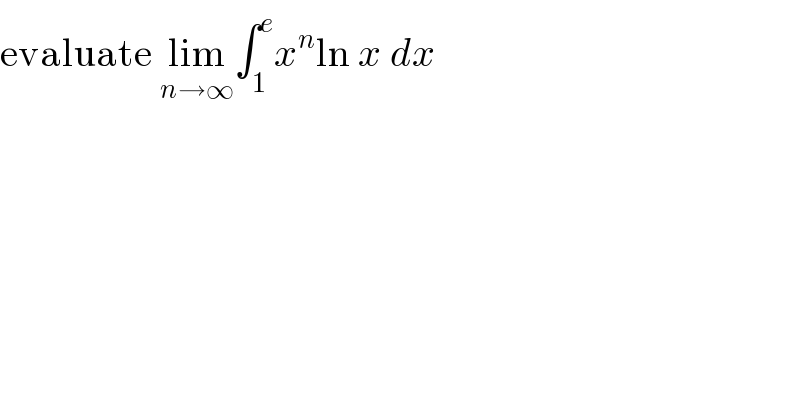
$$\mathrm{evaluate}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{1}} ^{{e}} {x}^{{n}} \mathrm{ln}\:{x}\:{dx}\: \\ $$
Commented by Dwaipayan Shikari last updated on 25/Jun/20

$$\infty \\ $$
Answered by Ar Brandon last updated on 25/Jun/20
![Let I=∫_1 ^e x^n lnxdx let { ((u=lnx)),((dv=x^n dx)) :}⇒ { ((du=(1/x)dx)),((v=(x^(n+1) /(n+1)))) :} ⇒I=[(x^(n+1) /(n+1))∙lnx]_1 ^e −(1/(n+1))∫_1 ^e x^n dx=(e^(n+1) /(n+1))−[(x^(n+1) /((n+1)^2 ))]_1 ^e ⇒I=(e^(n+1) /(n+1))−(e^(n+1) /((n+1)^2 ))+(1/((n+1)^2 )) lim_(n→∞) (I)=lim_(n→∞) {(e^(n+1) /1)−(e^(n+1) /(2(n+1)))}=lim_(n→∞) {e^(n+1) −(e^(n+1) /2)} =lim_(n→∞) {(e^(n+1) /2)}=+∞](https://www.tinkutara.com/question/Q100224.png)
$$\mathrm{Let}\:\mathcal{I}=\int_{\mathrm{1}} ^{\mathrm{e}} \mathrm{x}^{\mathrm{n}} \mathrm{lnxdx} \\ $$$$\mathrm{let}\:\begin{cases}{\mathrm{u}=\mathrm{lnx}}\\{\mathrm{dv}=\mathrm{x}^{\mathrm{n}} \mathrm{dx}}\end{cases}\Rightarrow\begin{cases}{\mathrm{du}=\frac{\mathrm{1}}{\mathrm{x}}\mathrm{dx}}\\{\mathrm{v}=\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}}\end{cases} \\ $$$$\Rightarrow\mathcal{I}=\left[\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\centerdot\mathrm{lnx}\right]_{\mathrm{1}} ^{\mathrm{e}} −\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\int_{\mathrm{1}} ^{\mathrm{e}} \mathrm{x}^{\mathrm{n}} \mathrm{dx}=\frac{\mathrm{e}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}−\left[\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\right]_{\mathrm{1}} ^{\mathrm{e}} \\ $$$$\Rightarrow\mathcal{I}=\frac{\mathrm{e}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{e}^{\mathrm{n}+\mathrm{1}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathcal{I}\right)=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left\{\frac{\mathrm{e}^{\mathrm{n}+\mathrm{1}} }{\mathrm{1}}−\frac{\mathrm{e}^{\mathrm{n}+\mathrm{1}} }{\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)}\right\}=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left\{\mathrm{e}^{\mathrm{n}+\mathrm{1}} −\frac{\mathrm{e}^{\mathrm{n}+\mathrm{1}} }{\mathrm{2}}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left\{\frac{\mathrm{e}^{\mathrm{n}+\mathrm{1}} }{\mathrm{2}}\right\}=+\infty \\ $$
Commented by DGmichael last updated on 25/Jun/20
�� LIATE
Commented by Ar Brandon last updated on 25/Jun/20
Ouais�� c'est ça.
Answered by mathmax by abdo last updated on 25/Jun/20
![A_n =∫_1 ^e x^n lnx dx changement lnx =t give A_n =∫_0 ^1 e^(nt) t e^(t ) dt =∫_0 ^1 t e^((n+1)t) dt =[(1/(n+1))t e^((n+1)t) ]_0 ^1 −∫_0 ^1 (1/(n+1))e^((n+1)t) dt =(e^(n+1) /(n+1)) −(1/((n+1)^2 ))[e^()n+1)t) ]_0 ^(1 ) =(e^(n+1) /(n+1))−(1/((n+1)^2 ))(e^(n+1) −1) =(e^(n+1) /(n+1))−(e^(n+1) /((n+1)^2 )) +(1/((n+1)^2 )) =(((n+1)e^(n+1) −e^(n+1) )/((n+1)^2 )) +(1/((n+1)^2 )) =((ne^(n+1) )/((n+1)^2 ))+(1/((n+1)^2 )) ⇒ lim_(n→+∞) A_n =lim_(n→+∞) ((ne^(n+1) )/((n+1)^2 )) =+∞](https://www.tinkutara.com/question/Q100229.png)
$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{1}} ^{\mathrm{e}} \:\mathrm{x}^{\mathrm{n}} \:\mathrm{lnx}\:\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{lnx}\:=\mathrm{t}\:\mathrm{give}\:\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{e}^{\mathrm{nt}} \:\mathrm{t}\:\mathrm{e}^{\mathrm{t}\:} \mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{t}\:\mathrm{e}^{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{t}} \:\mathrm{dt}\:\:=\left[\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\mathrm{t}\:\mathrm{e}^{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\mathrm{e}^{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{t}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{e}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\:\:\:\:−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\left[\mathrm{e}^{\left.\right)\left.\mathrm{n}+\mathrm{1}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\mathrm{1}\:} \:=\frac{\mathrm{e}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\left(\mathrm{e}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}\right) \\ $$$$=\frac{\mathrm{e}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{e}^{\mathrm{n}+\mathrm{1}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{e}^{\mathrm{n}+\mathrm{1}} −\mathrm{e}^{\mathrm{n}+\mathrm{1}} \:}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{ne}^{\mathrm{n}+\mathrm{1}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{A}_{\mathrm{n}} \:=\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\frac{\mathrm{ne}^{\mathrm{n}+\mathrm{1}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=+\infty \\ $$
