Question Number 89092 by 174 last updated on 15/Apr/20
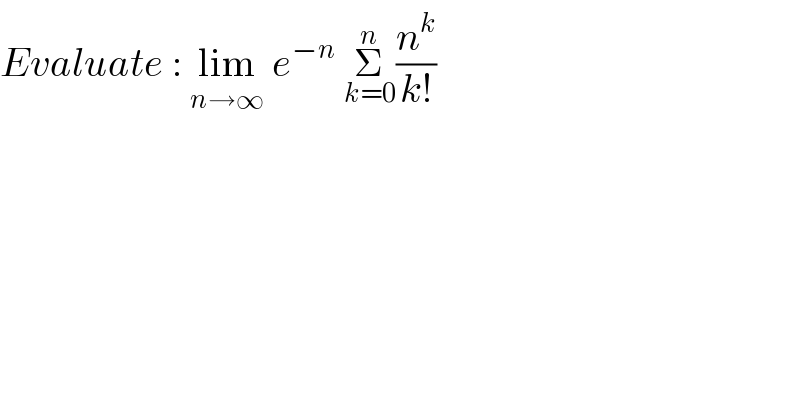
$${Evaluate}\::\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{e}^{−{n}} \:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{n}^{{k}} }{{k}!} \\ $$
Commented by abdomathmax last updated on 15/Apr/20
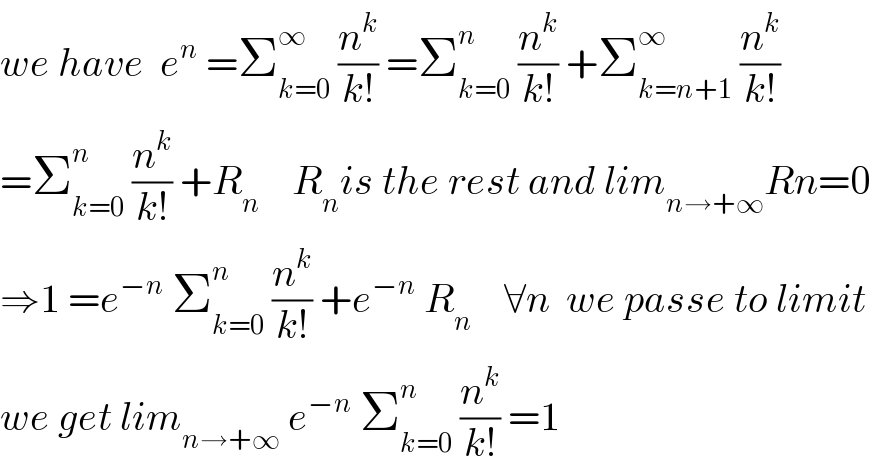
$${we}\:{have}\:\:{e}^{{n}} \:=\sum_{{k}=\mathrm{0}} ^{\infty} \:\frac{{n}^{{k}} }{{k}!}\:=\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{{n}^{{k}} }{{k}!}\:+\sum_{{k}={n}+\mathrm{1}} ^{\infty} \:\frac{{n}^{{k}} }{{k}!} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{{n}^{{k}} }{{k}!}\:+{R}_{{n}} \:\:\:\:{R}_{{n}} {is}\:{the}\:{rest}\:{and}\:{lim}_{{n}\rightarrow+\infty} {Rn}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}\:={e}^{−{n}} \:\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{{n}^{{k}} }{{k}!}\:+{e}^{−{n}} \:{R}_{{n}} \:\:\:\:\forall{n}\:\:{we}\:{passe}\:{to}\:{limit} \\ $$$${we}\:{get}\:{lim}_{{n}\rightarrow+\infty} \:{e}^{−{n}} \:\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{{n}^{{k}} }{{k}!}\:=\mathrm{1} \\ $$
Commented by 174 last updated on 15/Apr/20
thanks
