Question Number 112492 by mathdave last updated on 08/Sep/20
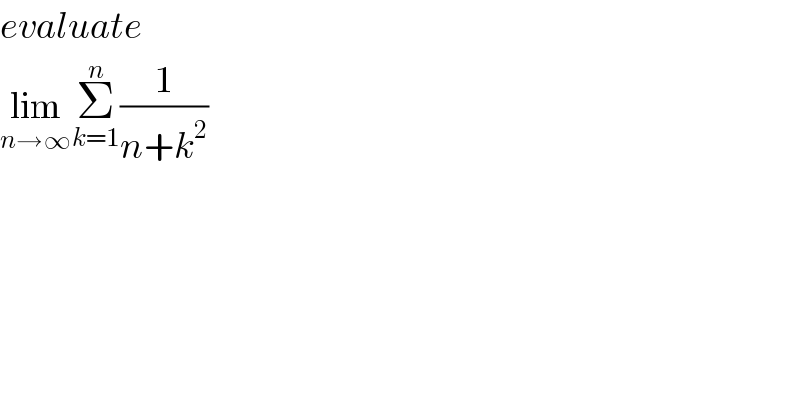
$${evaluate} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{n}+{k}^{\mathrm{2}} } \\ $$
Answered by Ar Brandon last updated on 08/Sep/20

$$\mathrm{1}\leqslant\mathrm{k}\leqslant\mathrm{n}\Rightarrow\mathrm{1}\leqslant\mathrm{k}^{\mathrm{2}} \leqslant\mathrm{n}^{\mathrm{2}} \Rightarrow\mathrm{n}+\mathrm{1}\leqslant\mathrm{n}+\mathrm{k}^{\mathrm{2}} \leqslant\mathrm{n}+\mathrm{n}^{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{n}+\mathrm{n}^{\mathrm{2}} }\leqslant\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}^{\mathrm{2}} }\leqslant\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\Rightarrow\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}+\mathrm{n}^{\mathrm{2}} }\leqslant\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}A}_{\mathrm{n}} \leqslant\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}} \\ $$$$\Rightarrow\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{n}}{\mathrm{n}+\mathrm{n}^{\mathrm{2}} }\leqslant\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}A}_{\mathrm{n}} \leqslant\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{n}}{\mathrm{n}+\mathrm{1}}\Rightarrow\mathrm{0}\leqslant\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\leqslant\mathrm{1} \\ $$$$… \\ $$
Commented by mathdave last updated on 08/Sep/20

$${nice}\:{attempt} \\ $$
