Menu Close

Evaluate-lim-x-0-tan-x-sin-x-sin-3-x-

Tinku Tara 0 Comments
Pin




Question Number 184792 by Spillover last updated on 11/Jan/23
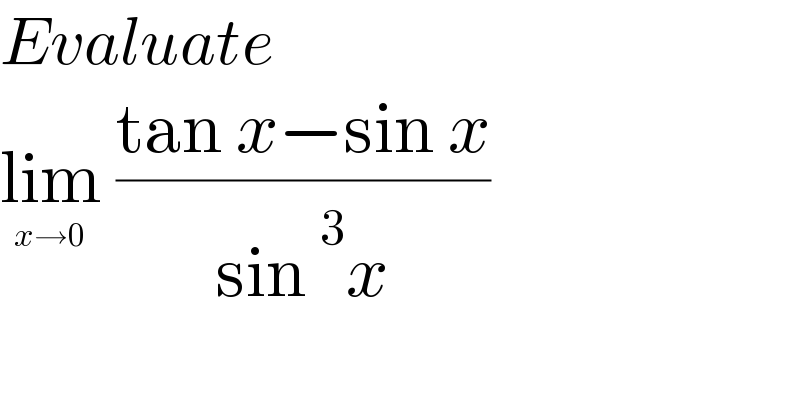
Evaluate lim_(x→0) ((tan x−sin x)/(sin^3 x))
$${Evaluate}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:{x}−\mathrm{sin}\:{x}}{\mathrm{sin}\:^{\mathrm{3}} {x}} \\ $$$$ \\ $$
Commented by MJS_new last updated on 11/Jan/23
(1/2)
$$\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Spillover last updated on 11/Jan/23
thank you
$${thank}\:{you} \\ $$
Answered by aba last updated on 12/Jan/23
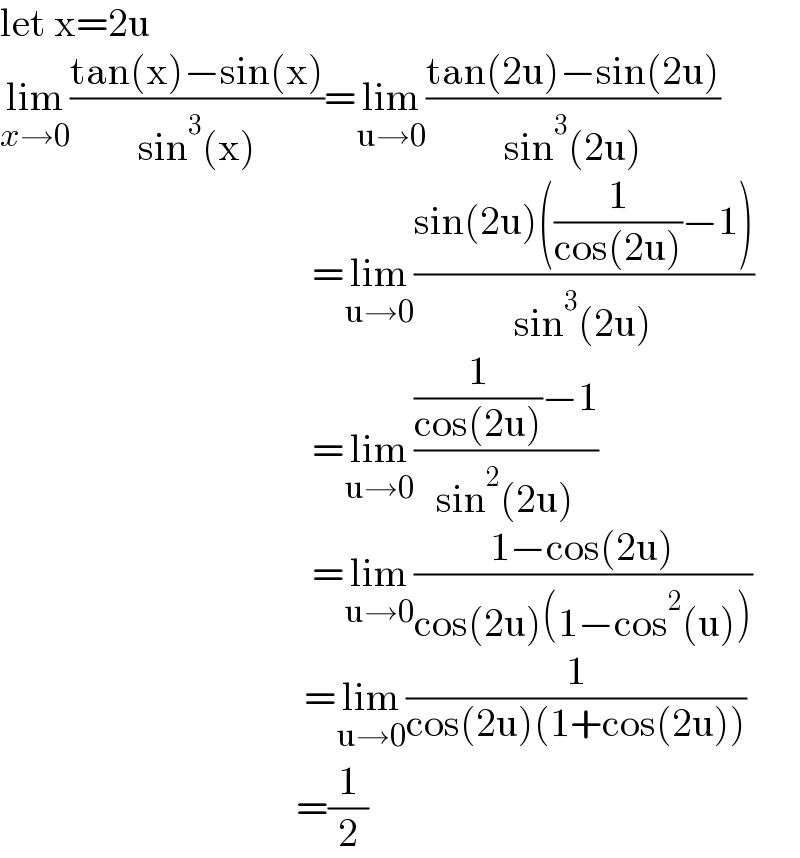
let x=2u lim_(x→0) ((tan(x)−sin(x))/(sin^3 (x)))=lim_(u→0) ((tan(2u)−sin(2u))/(sin^3 (2u))) =lim_(u→0) ((sin(2u)((1/(cos(2u)))−1))/(sin^3 (2u))) =lim_(u→0) (((1/(cos(2u)))−1)/(sin^2 (2u))) =lim_(u→0) ((1−cos(2u))/(cos(2u)(1−cos^2 (u)))) =lim_(u→0) (1/(cos(2u)(1+cos(2u)))) =(1/2)
$$\mathrm{let}\:\mathrm{x}=\mathrm{2u} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}\left(\mathrm{x}\right)−\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{sin}^{\mathrm{3}} \left(\mathrm{x}\right)}=\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}\left(\mathrm{2u}\right)−\mathrm{sin}\left(\mathrm{2u}\right)}{\mathrm{sin}^{\mathrm{3}} \left(\mathrm{2u}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\left(\mathrm{2u}\right)\left(\frac{\mathrm{1}}{\mathrm{cos}\left(\mathrm{2u}\right)}−\mathrm{1}\right)}{\mathrm{sin}^{\mathrm{3}} \left(\mathrm{2u}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{cos}\left(\mathrm{2u}\right)}−\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2u}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2u}\right)}{\mathrm{cos}\left(\mathrm{2u}\right)\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \left(\mathrm{u}\right)\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{cos}\left(\mathrm{2u}\right)\left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2u}\right)\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *