Question Number 173729 by a.lgnaoui last updated on 17/Jul/22
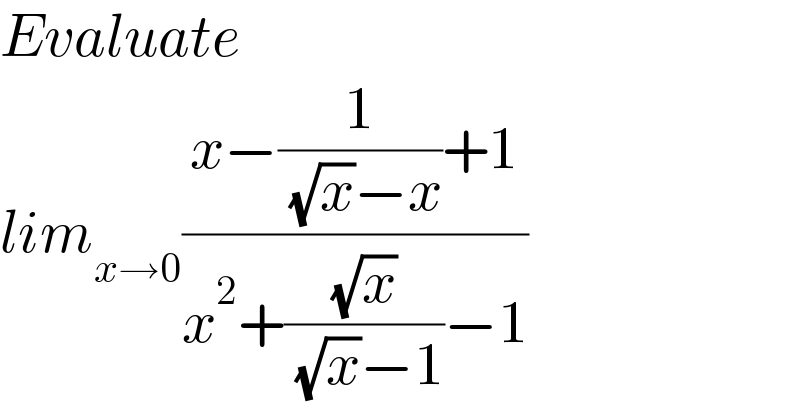
$${Evaluate} \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \frac{{x}−\frac{\mathrm{1}}{\:\sqrt{{x}}−{x}}+\mathrm{1}}{{x}^{\mathrm{2}} +\frac{\sqrt{{x}}}{\:\sqrt{{x}}−\mathrm{1}}−\mathrm{1}} \\ $$
Answered by blackmamba last updated on 17/Jul/22

$$\:\:{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{{x}−\frac{\mathrm{1}}{\:\sqrt{{x}}−{x}}\:−\mathrm{1}}{{x}^{\mathrm{2}} +\frac{\sqrt{{x}}}{\:\sqrt{{x}}−\mathrm{1}}−\mathrm{1}}\right) \\ $$$$\:\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\left({x}−\mathrm{1}\right)+\frac{\mathrm{1}}{\:\sqrt{{x}}\left(\sqrt{{x}}−\mathrm{1}\right)}}{\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)+\frac{\sqrt{{x}}}{\:\sqrt{{x}}−\mathrm{1}}}\right).\left(\frac{\sqrt{{x}}−\mathrm{1}}{\:\sqrt{{x}}−\mathrm{1}}\right) \\ $$$$\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\left(\sqrt{{x}}−\mathrm{1}\right)^{\mathrm{2}} \left(\sqrt{{x}}+\mathrm{1}\right)+\frac{\mathrm{1}}{\:\sqrt{{x}}}}{\left(\sqrt{{x}}−\mathrm{1}\right)^{\mathrm{2}} \left(\sqrt{{x}}+\mathrm{1}\right)\left({x}+\mathrm{1}\right)+\sqrt{{x}}}\right) \\ $$$$\:=\:\infty \\ $$$$ \\ $$
Answered by greougoury555 last updated on 17/Jul/22
![= lim_(x→0) ((((x+1)+(1/( (√x) ((√x)−1))))/((x−1)(x+1)+((√x)/( (√x)−1)))) ) [ let (1/( (√x)−1)) = t ; (√x) = ((1+t)/t) ] = lim_(t→−1) ((((((1+t)/t))^2 +1+(t^2 /(1+t)))/([(((1+t)/t))^2 −1][(((1+t)/t))^2 +1]+1+t))) =−∞](https://www.tinkutara.com/question/Q173731.png)
$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\left({x}+\mathrm{1}\right)+\frac{\mathrm{1}}{\:\sqrt{{x}}\:\left(\sqrt{{x}}−\mathrm{1}\right)}}{\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)+\frac{\sqrt{{x}}}{\:\sqrt{{x}}−\mathrm{1}}}\:\right) \\ $$$$\:\left[\:{let}\:\frac{\mathrm{1}}{\:\sqrt{{x}}−\mathrm{1}}\:=\:{t}\:;\:\sqrt{{x}}\:=\:\frac{\mathrm{1}+{t}}{{t}}\:\right]\: \\ $$$$=\:\underset{{t}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:\left(\frac{\left(\frac{\mathrm{1}+{t}}{{t}}\right)^{\mathrm{2}} +\mathrm{1}+\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}}}{\left[\left(\frac{\mathrm{1}+{t}}{{t}}\right)^{\mathrm{2}} −\mathrm{1}\right]\left[\left(\frac{\mathrm{1}+{t}}{{t}}\right)^{\mathrm{2}} +\mathrm{1}\right]+\mathrm{1}+{t}}\right) \\ $$$$=−\infty \\ $$
Commented by a.lgnaoui last updated on 17/Jul/22
$${thanks}\:{for}\:{you} \\ $$$$ \\ $$$$ \\ $$
