Question Number 85127 by Rio Michael last updated on 19/Mar/20

$$\mathrm{evaluate}: \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt{{x}}\:\mathrm{ln}\left(\mathrm{sin}\:{x}\right) \\ $$$$ \\ $$
Commented by john santu last updated on 19/Mar/20
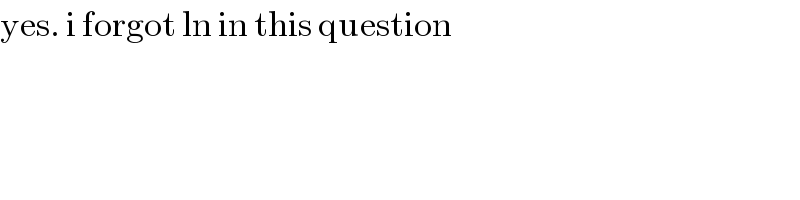
$$\mathrm{yes}.\:\mathrm{i}\:\mathrm{forgot}\:\mathrm{ln}\:\mathrm{in}\:\mathrm{this}\:\mathrm{question} \\ $$
Commented by MJS last updated on 19/Mar/20

$$\mathrm{there}'\mathrm{s}\:\mathrm{something}\:\mathrm{wrong} \\ $$
Commented by jagoll last updated on 19/Mar/20
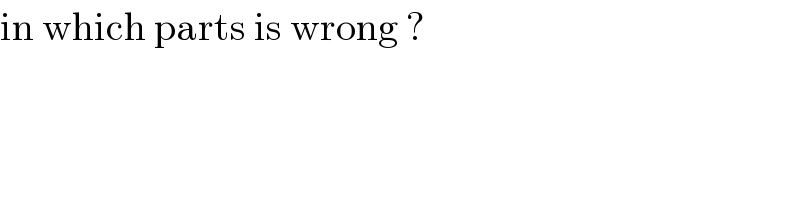
$$\mathrm{in}\:\mathrm{which}\:\mathrm{parts}\:\mathrm{is}\:\mathrm{wrong}\:? \\ $$
Commented by MJS last updated on 19/Mar/20
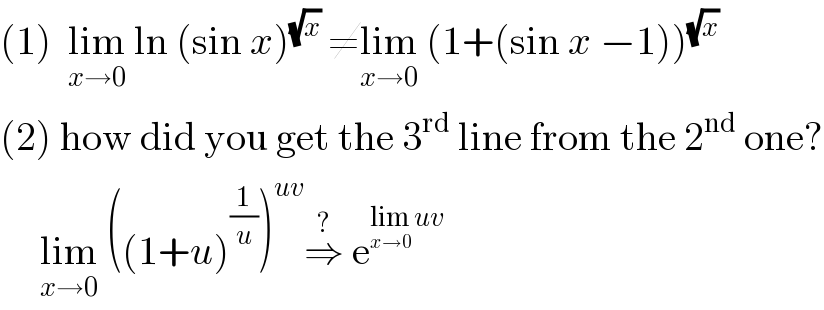
$$\left(\mathrm{1}\right)\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{ln}\:\left(\mathrm{sin}\:{x}\right)^{\sqrt{{x}}} \:\neq\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{1}+\left(\mathrm{sin}\:{x}\:−\mathrm{1}\right)\right)^{\sqrt{{x}}} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\mathrm{get}\:\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{line}\:\mathrm{from}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{one}? \\ $$$$\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\left(\mathrm{1}+{u}\right)^{\frac{\mathrm{1}}{{u}}} \right)^{{uv}} \overset{?} {\Rightarrow}\:\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{uv}} \\ $$
Answered by MJS last updated on 19/Mar/20
![L=lim_(x→0) (√x)ln sin x =lim_(x→0) ((xln sin x)/( (√x))) = =lim_(x→0) (((d/dx)[xln sin x])/((d/dx)[(√x)])) = lim_(x→0) (((x/(tan x))+ln sin x)/(1/(2(√x)))) = =2lim_(x→0) (((√x^3 )/(tan x))+(√x)ln sin x) ⇒ L=2L+2lim_(x→0) ((√x^3 )/(tan x)) ⇒ L=−2lim_(x→0) ((√x^3 )/(tan x)) =−2lim_(x→0) (((d/dx)[(√x^3 )])/((d/dx)[tan x])) = =−2lim_(x→0) (((3/2)(√x))/(1/(cos^2 x))) =−3lim_(x→0) (√x)cos^2 x =0](https://www.tinkutara.com/question/Q85147.png)
$${L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt{{x}}\mathrm{ln}\:\mathrm{sin}\:{x}\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\mathrm{ln}\:\mathrm{sin}\:{x}}{\:\sqrt{{x}}}\:= \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{{d}}{{dx}}\left[{x}\mathrm{ln}\:\mathrm{sin}\:{x}\right]}{\frac{{d}}{{dx}}\left[\sqrt{{x}}\right]}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{{x}}{\mathrm{tan}\:{x}}+\mathrm{ln}\:\mathrm{sin}\:{x}}{\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}\:= \\ $$$$=\mathrm{2}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\sqrt{{x}^{\mathrm{3}} }}{\mathrm{tan}\:{x}}+\sqrt{{x}}\mathrm{ln}\:\mathrm{sin}\:{x}\right) \\ $$$$\Rightarrow \\ $$$${L}=\mathrm{2}{L}+\mathrm{2}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{{x}^{\mathrm{3}} }}{\mathrm{tan}\:{x}} \\ $$$$\Rightarrow \\ $$$${L}=−\mathrm{2}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{{x}^{\mathrm{3}} }}{\mathrm{tan}\:{x}}\:=−\mathrm{2}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{{d}}{{dx}}\left[\sqrt{{x}^{\mathrm{3}} }\right]}{\frac{{d}}{{dx}}\left[\mathrm{tan}\:{x}\right]}\:= \\ $$$$=−\mathrm{2}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{3}}{\mathrm{2}}\sqrt{{x}}}{\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:{x}}}\:=−\mathrm{3}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt{{x}}\mathrm{cos}^{\mathrm{2}} \:{x}\:=\mathrm{0} \\ $$
Commented by Rio Michael last updated on 19/Mar/20

$${thanks}\:{y}'{all} \\ $$
