Question Number 184794 by Spillover last updated on 11/Jan/23
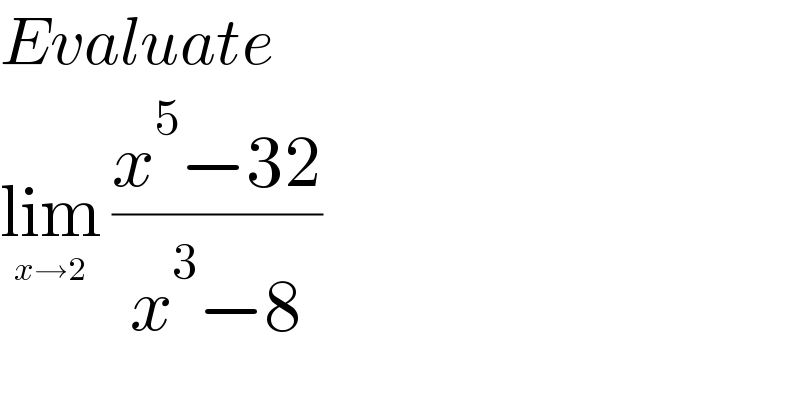
$${Evaluate}\: \\ $$$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{5}} −\mathrm{32}}{{x}^{\mathrm{3}} −\mathrm{8}} \\ $$
Commented by MJS_new last updated on 11/Jan/23

$$\frac{\mathrm{20}}{\mathrm{3}} \\ $$
Commented by Spillover last updated on 11/Jan/23

$${thank}\:{you} \\ $$
Answered by Spillover last updated on 12/Jan/23
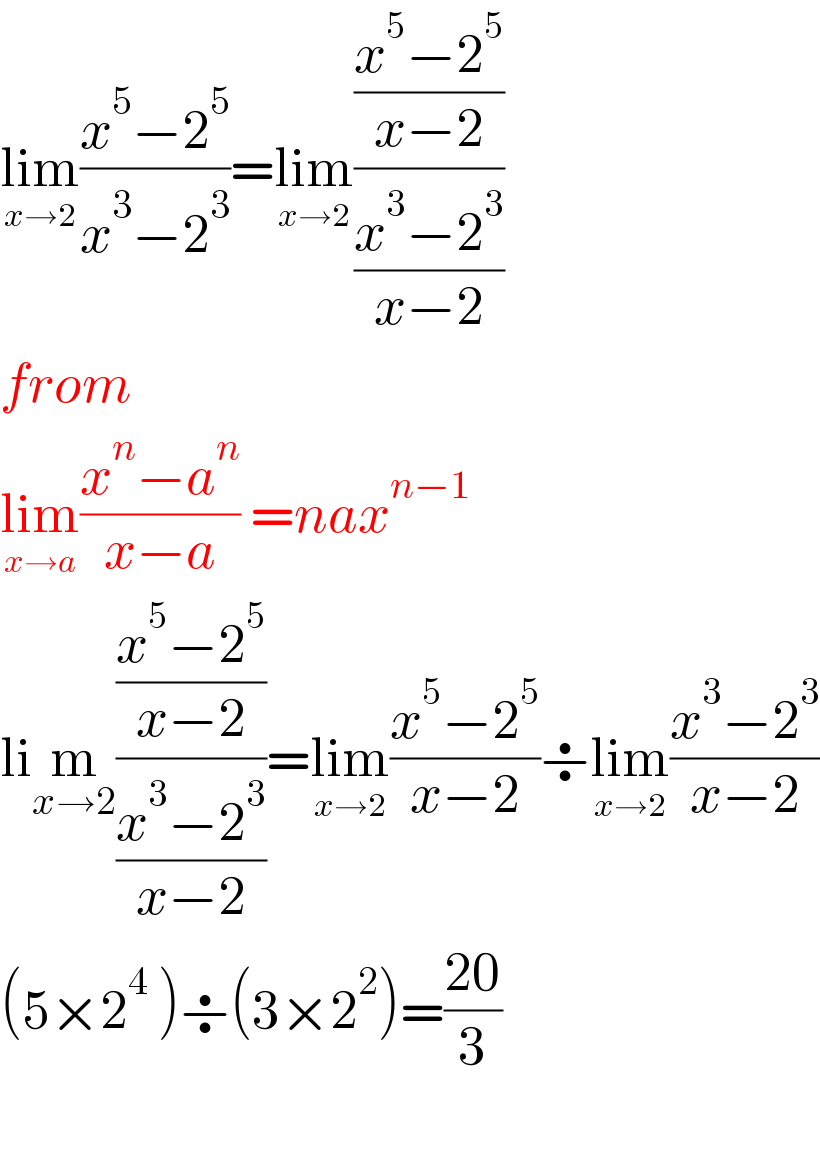
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{{x}^{\mathrm{5}} −\mathrm{2}^{\mathrm{5}} }{{x}^{\mathrm{3}} −\mathrm{2}^{\mathrm{3}} }=\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\frac{{x}^{\mathrm{5}} −\mathrm{2}^{\mathrm{5}} }{{x}−\mathrm{2}}}{\frac{{x}^{\mathrm{3}} −\mathrm{2}^{\mathrm{3}} }{{x}−\mathrm{2}}} \\ $$$${from} \\ $$$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{{x}^{{n}} −{a}^{{n}} }{{x}−{a}}\:={nax}^{{n}−\mathrm{1}} \\ $$$$\mathrm{li}\underset{{x}\rightarrow\mathrm{2}} {\mathrm{m}}\frac{\frac{{x}^{\mathrm{5}} −\mathrm{2}^{\mathrm{5}} }{{x}−\mathrm{2}}}{\frac{{x}^{\mathrm{3}} −\mathrm{2}^{\mathrm{3}} }{{x}−\mathrm{2}}}=\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{{x}^{\mathrm{5}} −\mathrm{2}^{\mathrm{5}} }{{x}−\mathrm{2}}\boldsymbol{\div}\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{{x}^{\mathrm{3}} −\mathrm{2}^{\mathrm{3}} }{{x}−\mathrm{2}} \\ $$$$\left(\mathrm{5}×\mathrm{2}^{\mathrm{4}} \:\right)\boldsymbol{\div}\left(\mathrm{3}×\mathrm{2}^{\mathrm{2}} \right)=\frac{\mathrm{20}}{\mathrm{3}} \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 12/Jan/23
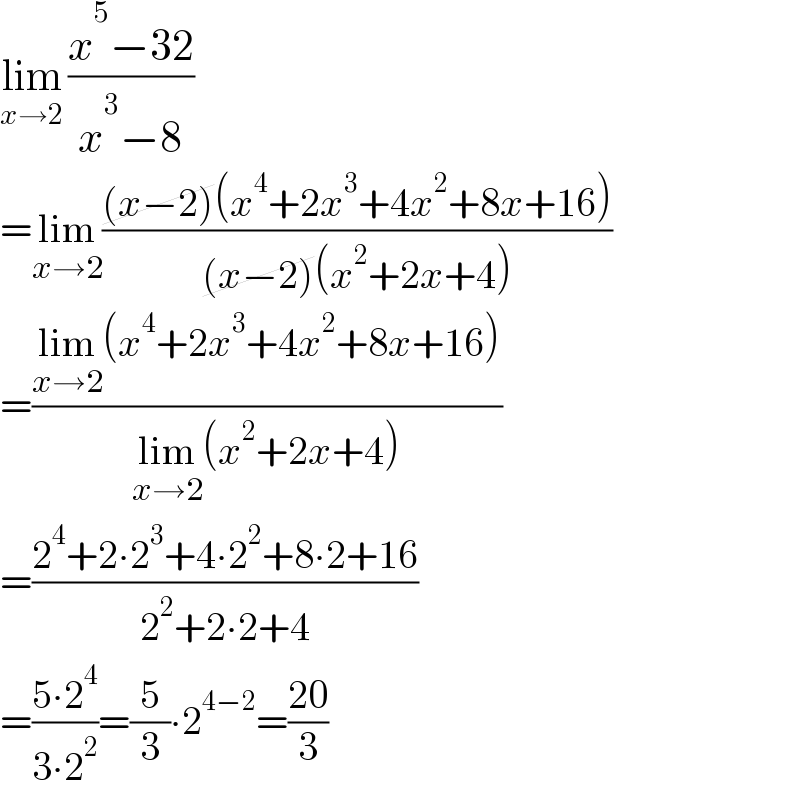
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{5}} −\mathrm{32}}{{x}^{\mathrm{3}} −\mathrm{8}} \\ $$$$=\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\cancel{\left({x}−\mathrm{2}\right)}\left({x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{16}\right)}{\cancel{\left({x}−\mathrm{2}\right)}\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\right)} \\ $$$$=\frac{\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\left({x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{16}\right)}{\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\right)} \\ $$$$=\frac{\mathrm{2}^{\mathrm{4}} +\mathrm{2}\centerdot\mathrm{2}^{\mathrm{3}} +\mathrm{4}\centerdot\mathrm{2}^{\mathrm{2}} +\mathrm{8}\centerdot\mathrm{2}+\mathrm{16}}{\mathrm{2}^{\mathrm{2}} +\mathrm{2}\centerdot\mathrm{2}+\mathrm{4}} \\ $$$$=\frac{\mathrm{5}\centerdot\mathrm{2}^{\mathrm{4}} }{\mathrm{3}\centerdot\mathrm{2}^{\mathrm{2}} }=\frac{\mathrm{5}}{\mathrm{3}}\centerdot\mathrm{2}^{\mathrm{4}−\mathrm{2}} =\frac{\mathrm{20}}{\mathrm{3}} \\ $$
Commented by Spillover last updated on 12/Jan/23
$${nice}\:{approach} \\ $$
Answered by BaliramKumar last updated on 14/Jan/23
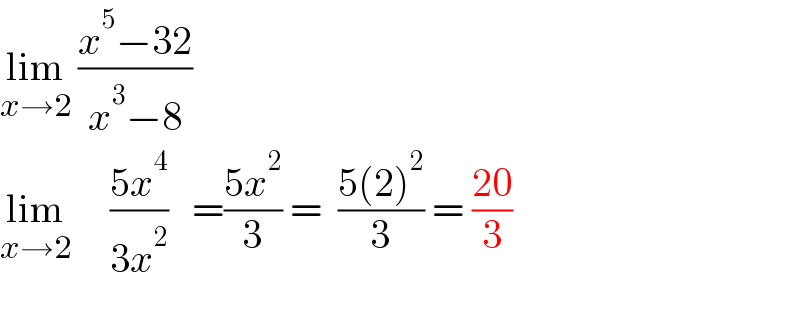
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{5}} −\mathrm{32}}{{x}^{\mathrm{3}} −\mathrm{8}} \\ $$$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\:\:\:\:\frac{\mathrm{5}{x}^{\mathrm{4}} }{\mathrm{3}{x}^{\mathrm{2}} }\:\:\:=\frac{\mathrm{5}{x}^{\mathrm{2}} }{\mathrm{3}}\:=\:\:\frac{\mathrm{5}\left(\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{3}}\:=\:\frac{\mathrm{20}}{\mathrm{3}} \\ $$$$ \\ $$
Answered by ajfour last updated on 14/Jan/23
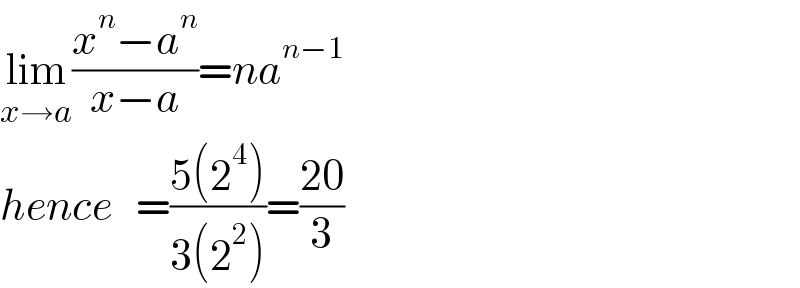
$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{{x}^{{n}} −{a}^{{n}} }{{x}−{a}}={na}^{{n}−\mathrm{1}} \\ $$$${hence}\:\:\:=\frac{\mathrm{5}\left(\mathrm{2}^{\mathrm{4}} \right)}{\mathrm{3}\left(\mathrm{2}^{\mathrm{2}} \right)}=\frac{\mathrm{20}}{\mathrm{3}} \\ $$
