evaluate-lim-x-f-x-and-lim-x-f-x-for-f-x-x-x-2-1-

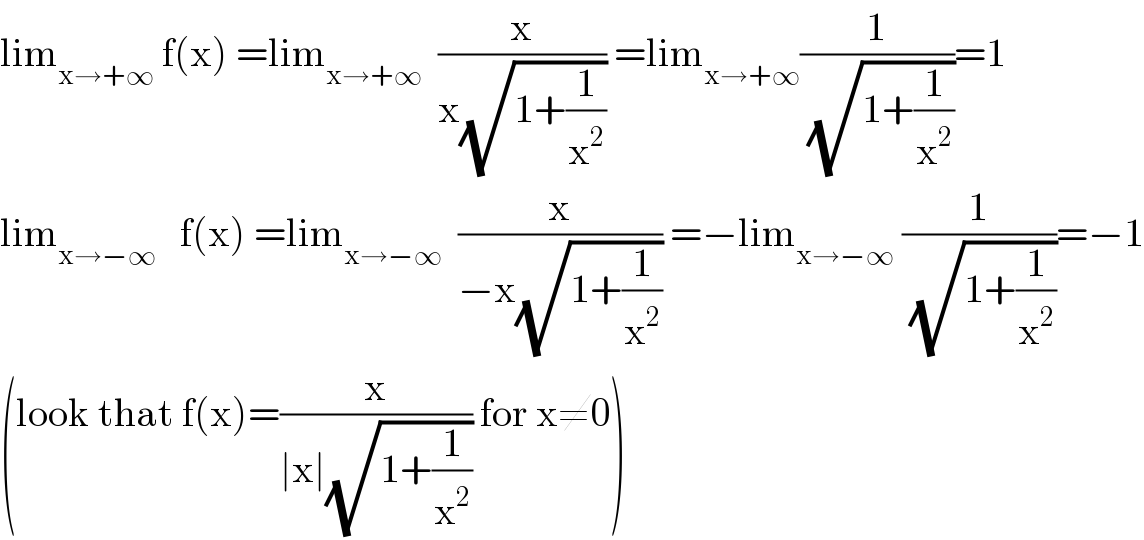
Question Number 120211 by bemath last updated on 30/Oct/20

e v a l u a t e \lim_{x \to \infty} f (x) a n d \lim_{x \to - \infty} f (x)

f o r f (x) = \frac{x}{\sqrt{x^{2} + 1}} .

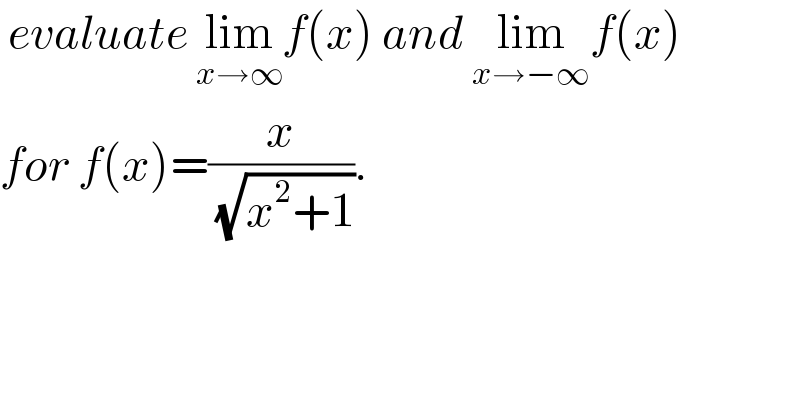
Answered by Ar Brandon last updated on 30/Oct/20

f (x) = \frac{x}{∣ x ∣ \sqrt{1 + \frac{1}{x^{2}}}} = \frac{sgn (x)}{\sqrt{1 + \frac{1}{x^{2}}}}

\lim_{x \to \infty} f (x) = 1, \lim_{x \to - \infty} f (x) = - 1

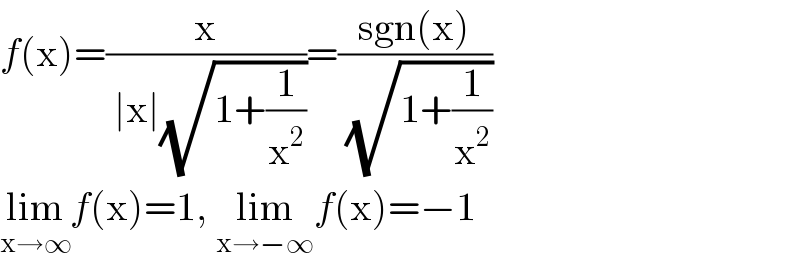
Commented by Dwaipayan Shikari last updated on 30/Oct/20

বাংলা শিখছো?

Commented by Ar Brandon last updated on 30/Oct/20

না, আমি কিছু মজা করছি��

Answered by benjo_mathlover last updated on 30/Oct/20

R e w r i t e t h e e x p r e s s i o n f o r

f (x) a s f o l l o w s : f (x) = \frac{x}{\sqrt{x^{2} (1 + \frac{1}{x^{2}})}}

f (x) = \frac{x}{\sqrt{x^{2}} \sqrt{1 + \frac{1}{x^{2}}}} = \frac{x}{∣ x ∣ \sqrt{1 + \frac{1}{x^{2}}}}

f (x) = \frac{s g n x}{\sqrt{1 + \frac{1}{x^{2}}}}; [w h e r e s g n x = \frac{x}{∣ x ∣} = {\begin{cases} 1, i f x > 0 \\ - 1, i f x < 0 \end{cases}

T h e f a c t o r \sqrt{1 + (1 / x^{2})} a p p r o a c h e s 1 a s x \to \infty o r - \infty

t h e r e f o r e {\begin{cases} \lim_{x \to \infty} f (x) = 1 \\ \lim_{x \to - \infty} f (x) = - 1 \end{cases}

Answered by mathmax by abdo last updated on 30/Oct/20

\lim_{x \to + \infty} f (x) = \lim_{x \to + \infty} \frac{x}{x \sqrt{1 + \frac{1}{x^{2}}}} = \lim_{x \to + \infty} \frac{1}{\sqrt{1 + \frac{1}{x^{2}}}} = 1

\lim_{x \to - \infty} f (x) = \lim_{x \to - \infty} \frac{x}{- x \sqrt{1 + \frac{1}{x^{2}}}} = - \lim_{x \to - \infty} \frac{1}{\sqrt{1 + \frac{1}{x^{2}}}} = - 1

(look that f (x) = \frac{x}{∣ x ∣ \sqrt{1 + \frac{1}{x^{2}}}} for x \neq 0)