Question Number 184018 by paul2222 last updated on 01/Jan/23
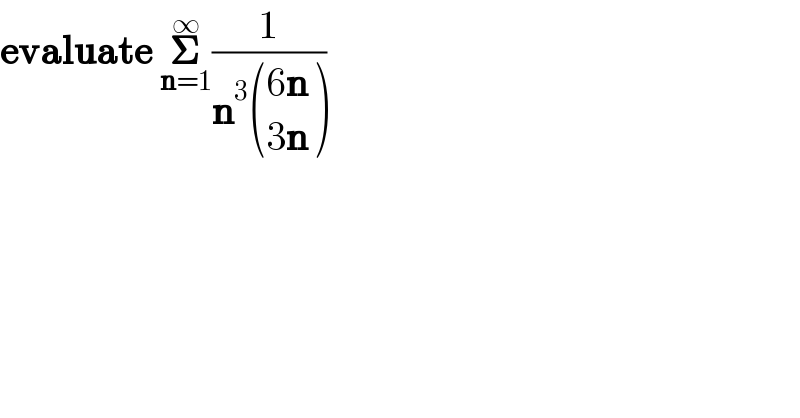
$$\boldsymbol{\mathrm{evaluate}}\:\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\boldsymbol{\sum}}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}^{\mathrm{3}} \begin{pmatrix}{\mathrm{6}\boldsymbol{\mathrm{n}}}\\{\mathrm{3}\boldsymbol{\mathrm{n}}}\end{pmatrix}} \\ $$
Answered by witcher3 last updated on 02/Jan/23
![Σ_(n≥1) ((((3n)!)^2 )/(n^3 .(6n)!))=Σ_(n≥1) Π_(k=0) ^(n−1) (((3k+1)^2 (3k+2)^2 (3k+3)^2 )/((6k+1)(6k+2)(6k+3)(6k+4)(6k+5)(6k+6)n^3 )) =Σ_(n≥1) Π_(k=0) ^(n−1) (((3k+1)(3k+2)(3k+3))/((6k+1)(6k+3)(6k+5).8.n^3 ))∴n−1=m =(1/(20))+Σ_(m≥1) Π_(k=0) ^m (((k+(1/3))(k+(2/3))(k+1))/(64.(k+(1/6))(k+(1/2))(k+(5/6)).(m+1)^3 )) =(1/(20))+Σ_(m≥1) (1/(20))Π_(k=1) ^m (((k+(1/3))(k+(2/3))(k+1)k^3 )/(64(k+(1/6))(k+(1/2))(k+(5/6)).(k+1)^3 )) =(1/(20))(1+Σ_(m≥1) Π_(k=0) ^(m−1) (((k+(4/3))(k+(5/3))(k+2)(k+1)^3 )/(64(k+(7/6))(k+(9/6))(k+((11)/6))(k+2)^2 )).(1/(m!))) =(1/(20))(1+Σ_(m≥1) ((((4/3))_m ((5/3))_m (2)_m (1)_m (1)_m (1)_m )/(((7/6))_m ((3/2))_m (((11)/6))_m (2)_m (2)_m )).((((1/(64)))^m )/(m!))) =(1/(20)). _6 F_5 ((4/3),(5/3),2,1,1,1;(7/6),(3/2),((11)/6),2,2;[(1/(64))]) _p F_q (.....) Hyper Geometric Function](https://www.tinkutara.com/question/Q184082.png)
$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(\left(\mathrm{3}{n}\right)!\right)^{\mathrm{2}} }{{n}^{\mathrm{3}} .\left(\mathrm{6}{n}\right)!}=\underset{{n}\geqslant\mathrm{1}} {\sum}\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\frac{\left(\mathrm{3}{k}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{3}{k}+\mathrm{2}\right)^{\mathrm{2}} \left(\mathrm{3}{k}+\mathrm{3}\right)^{\mathrm{2}} }{\left(\mathrm{6}{k}+\mathrm{1}\right)\left(\mathrm{6}{k}+\mathrm{2}\right)\left(\mathrm{6}{k}+\mathrm{3}\right)\left(\mathrm{6}{k}+\mathrm{4}\right)\left(\mathrm{6}{k}+\mathrm{5}\right)\left(\mathrm{6}{k}+\mathrm{6}\right){n}^{\mathrm{3}} } \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\frac{\left(\mathrm{3}{k}+\mathrm{1}\right)\left(\mathrm{3}{k}+\mathrm{2}\right)\left(\mathrm{3}{k}+\mathrm{3}\right)}{\left(\mathrm{6}{k}+\mathrm{1}\right)\left(\mathrm{6}{k}+\mathrm{3}\right)\left(\mathrm{6}{k}+\mathrm{5}\right).\mathrm{8}.{n}^{\mathrm{3}} }\therefore{n}−\mathrm{1}={m} \\ $$$$=\frac{\mathrm{1}}{\mathrm{20}}+\underset{{m}\geqslant\mathrm{1}} {\sum}\underset{{k}=\mathrm{0}} {\overset{{m}} {\prod}}\frac{\left({k}+\frac{\mathrm{1}}{\mathrm{3}}\right)\left({k}+\frac{\mathrm{2}}{\mathrm{3}}\right)\left({k}+\mathrm{1}\right)}{\mathrm{64}.\left({k}+\frac{\mathrm{1}}{\mathrm{6}}\right)\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left({k}+\frac{\mathrm{5}}{\mathrm{6}}\right).\left({m}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{20}}+\underset{{m}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\mathrm{20}}\underset{{k}=\mathrm{1}} {\overset{{m}} {\prod}}\frac{\left({k}+\frac{\mathrm{1}}{\mathrm{3}}\right)\left({k}+\frac{\mathrm{2}}{\mathrm{3}}\right)\left({k}+\mathrm{1}\right){k}^{\mathrm{3}} }{\mathrm{64}\left({k}+\frac{\mathrm{1}}{\mathrm{6}}\right)\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left({k}+\frac{\mathrm{5}}{\mathrm{6}}\right).\left({k}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{20}}\left(\mathrm{1}+\underset{{m}\geqslant\mathrm{1}} {\sum}\underset{{k}=\mathrm{0}} {\overset{{m}−\mathrm{1}} {\prod}}\frac{\left({k}+\frac{\mathrm{4}}{\mathrm{3}}\right)\left({k}+\frac{\mathrm{5}}{\mathrm{3}}\right)\left({k}+\mathrm{2}\right)\left({k}+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{64}\left({k}+\frac{\mathrm{7}}{\mathrm{6}}\right)\left({k}+\frac{\mathrm{9}}{\mathrm{6}}\right)\left({k}+\frac{\mathrm{11}}{\mathrm{6}}\right)\left({k}+\mathrm{2}\right)^{\mathrm{2}} }.\frac{\mathrm{1}}{{m}!}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{20}}\left(\mathrm{1}+\underset{{m}\geqslant\mathrm{1}} {\sum}\frac{\left(\frac{\mathrm{4}}{\mathrm{3}}\right)_{{m}} \left(\frac{\mathrm{5}}{\mathrm{3}}\right)_{{m}} \left(\mathrm{2}\right)_{{m}} \left(\mathrm{1}\right)_{{m}} \left(\mathrm{1}\right)_{{m}} \left(\mathrm{1}\right)_{{m}} }{\left(\frac{\mathrm{7}}{\mathrm{6}}\right)_{{m}} \left(\frac{\mathrm{3}}{\mathrm{2}}\right)_{{m}} \left(\frac{\mathrm{11}}{\mathrm{6}}\right)_{{m}} \left(\mathrm{2}\right)_{{m}} \left(\mathrm{2}\right)_{{m}} }.\frac{\left(\frac{\mathrm{1}}{\mathrm{64}}\right)^{{m}} }{{m}!}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{20}}.\:\:\:_{\mathrm{6}} {F}_{\mathrm{5}} \left(\frac{\mathrm{4}}{\mathrm{3}},\frac{\mathrm{5}}{\mathrm{3}},\mathrm{2},\mathrm{1},\mathrm{1},\mathrm{1};\frac{\mathrm{7}}{\mathrm{6}},\frac{\mathrm{3}}{\mathrm{2}},\frac{\mathrm{11}}{\mathrm{6}},\mathrm{2},\mathrm{2};\left[\frac{\mathrm{1}}{\mathrm{64}}\right]\right) \\ $$$$\:\:_{{p}} {F}_{{q}} \left(…..\right)\:{Hyper}\:{Geometric}\:{Function} \\ $$
Commented by paul2222 last updated on 02/Jan/23

$$\boldsymbol{\mathrm{nice}}\:\boldsymbol{\mathrm{solution}}\:\boldsymbol{\mathrm{sir}} \\ $$
Commented by witcher3 last updated on 06/Jan/23
$${thank}\:{You}\:{have}\:{a}\:{good}\:{day} \\ $$$$ \\ $$
