Question Number 100320 by bemath last updated on 26/Jun/20
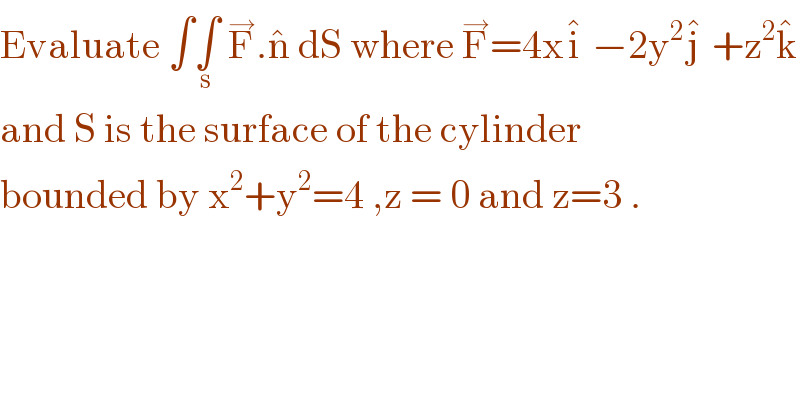
$$\mathrm{Evaluate}\:\int\underset{\mathrm{s}} {\int}\:\overset{\rightarrow} {\mathrm{F}}.\hat {\mathrm{n}}\:\mathrm{dS}\:\mathrm{where}\:\overset{\rightarrow} {\mathrm{F}}=\mathrm{4x}\hat {\mathrm{i}}\:−\mathrm{2y}^{\mathrm{2}} \hat {\mathrm{j}}\:+\mathrm{z}^{\mathrm{2}} \hat {\mathrm{k}}\: \\ $$$$\mathrm{and}\:\mathrm{S}\:\mathrm{is}\:\mathrm{the}\:\mathrm{surface}\:\mathrm{of}\:\mathrm{the}\:\mathrm{cylinder} \\ $$$$\mathrm{bounded}\:\mathrm{by}\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{4}\:,\mathrm{z}\:=\:\mathrm{0}\:\mathrm{and}\:\mathrm{z}=\mathrm{3}\:. \\ $$
Answered by smridha last updated on 26/Jun/20
![∫∫_s F^→ .n^� ds=∫∫_R F^→ .n^� ((dxdz)/(∣n^� .j^� ∣)) [ take a projection on x−z plane] our scaler point f^n 𝚽=x^2 +y^2 −4 so the unit normal of this surface n^� =((▽𝚽)/(∣▽𝚽∣))=((xi^� +yj^� )/2) so ∣n^� .j^� ∣=(y/2) and F^→ .n^� =((4x^2 −2y^3 )/2). now our integral looks like ∫_0 ^3 ∫_0 ^2 [((4x^2 )/y)−2y^2 ]dxdz =∫_0 ^3 dz[∫_0 ^2 (((4x^2 )/( (√(4−x^2 ))))+(2x^2 −8))dx] =3[−4.∫_0 ^2 {(√(4−x^2 )) −(4/( (√(4−x^2 ))))}dx+((2/3)x^3 −8x)_0 ^2 ] =3[−4(((x(√(4−x^2 )))/2)−2sin^(−1) ((x/2)))_0 ^2 +((16)/3)−16] =3[4𝛑−((32)/3)]=[12𝛑−32]](https://www.tinkutara.com/question/Q100350.png)
$$\int\int_{\boldsymbol{{s}}} \overset{\rightarrow} {\boldsymbol{{F}}}.\hat {\boldsymbol{{n}ds}}=\int\int_{\boldsymbol{{R}}} \overset{\rightarrow} {\boldsymbol{{F}}}.\hat {\boldsymbol{{n}}}\frac{{dx}\boldsymbol{{dz}}}{\mid\hat {\boldsymbol{{n}}}.\hat {\boldsymbol{{j}}}\mid}\:\left[\:\boldsymbol{{take}}\:\boldsymbol{{a}}\:\boldsymbol{{projection}}\:\boldsymbol{{on}}\:\boldsymbol{{x}}−\boldsymbol{{z}}\:\boldsymbol{{plane}}\right] \\ $$$$\boldsymbol{{our}}\:\boldsymbol{{scaler}}\:\boldsymbol{{point}}\:\boldsymbol{{f}}^{\boldsymbol{{n}}} \:\boldsymbol{\Phi}=\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} −\mathrm{4} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{the}}\:\boldsymbol{{unit}}\:\boldsymbol{{normal}}\:\boldsymbol{{of}}\:\boldsymbol{{this}}\:\boldsymbol{{surface}} \\ $$$$\hat {\boldsymbol{{n}}}=\frac{\bigtriangledown\boldsymbol{\Phi}}{\mid\bigtriangledown\boldsymbol{\Phi}\mid}=\frac{\boldsymbol{{x}}\hat {\boldsymbol{{i}}}+\boldsymbol{{y}}\hat {\boldsymbol{{j}}}}{\mathrm{2}}\:\boldsymbol{{so}}\:\mid\hat {\boldsymbol{{n}}}.\hat {\boldsymbol{{j}}}\mid=\frac{\boldsymbol{{y}}}{\mathrm{2}} \\ $$$$\boldsymbol{{and}}\:\overset{\rightarrow} {\boldsymbol{{F}}}.\hat {\boldsymbol{{n}}}=\frac{\mathrm{4}\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{y}}^{\mathrm{3}} }{\mathrm{2}}. \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{our}}\:\boldsymbol{{integral}}\:\boldsymbol{{looks}}\:\boldsymbol{{like}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{3}} \int_{\mathrm{0}} ^{\mathrm{2}} \left[\frac{\mathrm{4}\boldsymbol{{x}}^{\mathrm{2}} }{\boldsymbol{{y}}}−\mathrm{2}\boldsymbol{{y}}^{\mathrm{2}} \right]\boldsymbol{{dxdz}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{3}} \boldsymbol{{dz}}\left[\int_{\mathrm{0}} ^{\mathrm{2}} \left(\frac{\mathrm{4}\boldsymbol{{x}}^{\mathrm{2}} }{\:\sqrt{\mathrm{4}−\boldsymbol{{x}}^{\mathrm{2}} }}+\left(\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{8}\right)\right)\boldsymbol{{dx}}\right] \\ $$$$=\mathrm{3}\left[−\mathrm{4}.\int_{\mathrm{0}} ^{\mathrm{2}} \left\{\sqrt{\mathrm{4}−\boldsymbol{{x}}^{\mathrm{2}} }\:\:−\frac{\mathrm{4}}{\:\sqrt{\mathrm{4}−\boldsymbol{{x}}^{\mathrm{2}} }}\right\}\boldsymbol{{dx}}+\left(\frac{\mathrm{2}}{\mathrm{3}}\boldsymbol{{x}}^{\mathrm{3}} −\mathrm{8}\boldsymbol{{x}}\right)_{\mathrm{0}} ^{\mathrm{2}} \right] \\ $$$$=\mathrm{3}\left[−\mathrm{4}\left(\frac{\boldsymbol{{x}}\sqrt{\mathrm{4}−\boldsymbol{{x}}^{\mathrm{2}} }}{\mathrm{2}}−\mathrm{2sin}^{−\mathrm{1}} \left(\frac{\boldsymbol{{x}}}{\mathrm{2}}\right)\right)_{\mathrm{0}} ^{\mathrm{2}} +\frac{\mathrm{16}}{\mathrm{3}}−\mathrm{16}\right] \\ $$$$=\mathrm{3}\left[\mathrm{4}\boldsymbol{\pi}−\frac{\mathrm{32}}{\mathrm{3}}\right]=\left[\mathrm{12}\boldsymbol{\pi}−\mathrm{32}\right] \\ $$
Commented by bemath last updated on 26/Jun/20

$$\mathrm{great} \\ $$
