Question Number 104060 by bramlex last updated on 19/Jul/20
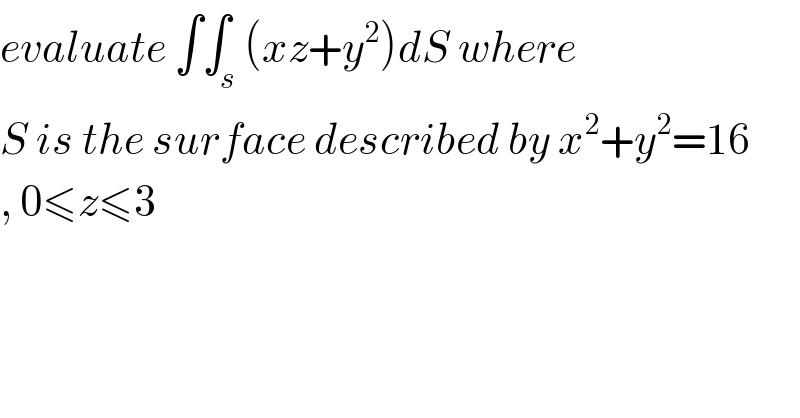
$${evaluate}\:\int\int_{{s}} \left({xz}+{y}^{\mathrm{2}} \right){dS}\:{where} \\ $$$${S}\:{is}\:{the}\:{surface}\:{described}\:{by}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{16} \\ $$$$,\:\mathrm{0}\leqslant{z}\leqslant\mathrm{3} \\ $$
Answered by john santu last updated on 19/Jul/20
![∫∫_s f(x,y,z)dS = ∫∫_R f(x,y,z)∣r_u ^→ ×r_v ^→ ∣dudv ⇒x=4cos θ , y=4sin θ r^→ (θ,z) = (((4cos θ)),((4sin θ)),(( z)) ) ,0≤θ≤2π , 0≤z≤3 . r_θ ^→ = (((−4sin θ)),(( 4 cos θ)),(( 0)) ) r_z ^→ = ((0),(0),(1) ) ; r_θ ^→ ×r_z ^→ = determinant (((−4sin θ 4cos θ 0)),(( 0 0 1)))= (4cos θ , 4sin θ ,0 ) ; ∣r_θ ^→ ×r_z ^→ ∣ = 4 S= ∫_0 ^(2π) ∫_0 ^3 [4z cos θ+16sin^2 θ] 4 dz dθ S= ∫_0 ^(2π) 4{(2z^2 cos θ+16z.sin^2 θ)}_0 ^3 dθ S= ∫_0 ^(2π) 4(18cos θ+48sin^2 θ )dθ S = 24∫_0 ^(2π) (3cos θ+8sin^2 θ) dθ S = 24∫_0 ^(2π) (3cos θ + 4−4cos 2θ) dθ S= 24 { 3sin θ+4θ−2sin 2θ} _0^(2π) S = 192π . (JS ⊛)](https://www.tinkutara.com/question/Q104124.png)
$$\int\int_{{s}} {f}\left({x},{y},{z}\right){dS}\:=\:\int\int_{{R}} {f}\left({x},{y},{z}\right)\mid\overset{\rightarrow} {{r}}_{{u}} ×\overset{\rightarrow} {{r}}_{{v}} \mid{dudv} \\ $$$$\Rightarrow{x}=\mathrm{4cos}\:\theta\:,\:{y}=\mathrm{4sin}\:\theta\: \\ $$$$\overset{\rightarrow} {{r}}\left(\theta,{z}\right)\:=\:\begin{pmatrix}{\mathrm{4cos}\:\theta}\\{\mathrm{4sin}\:\theta}\\{\:\:\:\:\:\:{z}}\end{pmatrix}\:,\mathrm{0}\leqslant\theta\leqslant\mathrm{2}\pi\:, \\ $$$$\mathrm{0}\leqslant{z}\leqslant\mathrm{3}\:.\:\overset{\rightarrow} {{r}}_{\theta} =\:\begin{pmatrix}{−\mathrm{4sin}\:\theta}\\{\:\:\:\mathrm{4}\:\mathrm{cos}\:\theta}\\{\:\:\:\:\:\:\:\mathrm{0}}\end{pmatrix} \\ $$$$\overset{\rightarrow} {{r}}_{{z}} \:=\:\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\\{\mathrm{1}}\end{pmatrix}\:\:;\:\overset{\rightarrow} {{r}}_{\theta} ×\overset{\rightarrow} {{r}}_{{z}} = \\ $$$$\begin{vmatrix}{−\mathrm{4sin}\:\theta\:\:\:\:\:\:\mathrm{4cos}\:\theta\:\:\:\:\:\:\:\mathrm{0}}\\{\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{vmatrix}=\:\left(\mathrm{4cos}\:\theta\right. \\ $$$$\left.,\:\mathrm{4sin}\:\theta\:,\mathrm{0}\:\right)\:;\:\mid\overset{\rightarrow} {{r}}_{\theta} ×\overset{\rightarrow} {{r}}_{{z}} \mid\:=\:\mathrm{4} \\ $$$${S}=\:\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\:\left[\mathrm{4}{z}\:\mathrm{cos}\:\theta+\mathrm{16sin}\:^{\mathrm{2}} \theta\right]\:\mathrm{4}\:{dz}\:{d}\theta \\ $$$${S}=\:\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\:\mathrm{4}\left\{\left(\mathrm{2}{z}^{\mathrm{2}} \:\mathrm{cos}\:\theta+\mathrm{16}{z}.\mathrm{sin}\:^{\mathrm{2}} \theta\right)\right\}_{\mathrm{0}} ^{\mathrm{3}} \:{d}\theta \\ $$$${S}=\:\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\:\mathrm{4}\left(\mathrm{18cos}\:\theta+\mathrm{48sin}\:^{\mathrm{2}} \theta\:\right){d}\theta \\ $$$${S}\:=\:\mathrm{24}\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\:\left(\mathrm{3cos}\:\theta+\mathrm{8sin}\:^{\mathrm{2}} \theta\right)\:{d}\theta \\ $$$${S}\:=\:\mathrm{24}\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\left(\mathrm{3cos}\:\theta\:+\:\mathrm{4}−\mathrm{4cos}\:\mathrm{2}\theta\right)\:{d}\theta \\ $$$${S}=\:\mathrm{24}\:\left\{\:\mathrm{3sin}\:\theta+\mathrm{4}\theta−\mathrm{2sin}\:\mathrm{2}\theta\right\}\:_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$${S}\:=\:\mathrm{192}\pi\:.\:\left({JS}\:\circledast\right)\:\: \\ $$$$ \\ $$
