Question Number 147837 by peter frank last updated on 23/Jul/21
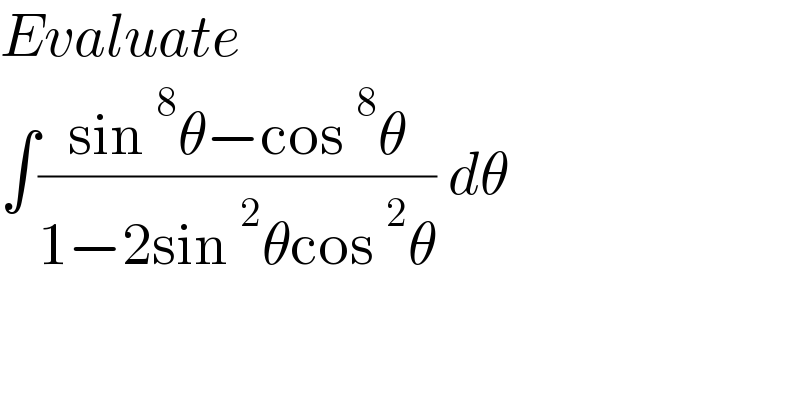
$${Evaluate} \\ $$$$\int\frac{\mathrm{sin}\:^{\mathrm{8}} \theta−\mathrm{cos}\:^{\mathrm{8}} \theta}{\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:^{\mathrm{2}} \theta}\:{d}\theta \\ $$$$ \\ $$
Answered by liberty last updated on 24/Jul/21
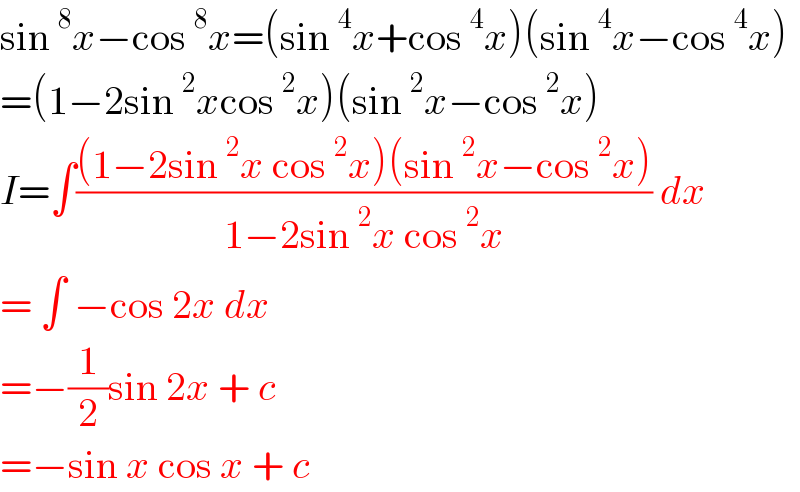
$$\mathrm{sin}\:^{\mathrm{8}} {x}−\mathrm{cos}\:^{\mathrm{8}} {x}=\left(\mathrm{sin}\:^{\mathrm{4}} {x}+\mathrm{cos}\:^{\mathrm{4}} {x}\right)\left(\mathrm{sin}\:^{\mathrm{4}} {x}−\mathrm{cos}\:^{\mathrm{4}} {x}\right) \\ $$$$=\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}\mathrm{cos}\:^{\mathrm{2}} {x}\right)\left(\mathrm{sin}\:^{\mathrm{2}} {x}−\mathrm{cos}\:^{\mathrm{2}} {x}\right) \\ $$$${I}=\int\frac{\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}\:\mathrm{cos}\:^{\mathrm{2}} {x}\right)\left(\mathrm{sin}\:^{\mathrm{2}} {x}−\mathrm{cos}\:^{\mathrm{2}} {x}\right)}{\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}\:\mathrm{cos}\:^{\mathrm{2}} {x}}\:{dx} \\ $$$$=\:\int\:−\mathrm{cos}\:\mathrm{2}{x}\:{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}{x}\:+\:{c} \\ $$$$=−\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}\:+\:{c}\: \\ $$
Commented by peter frank last updated on 24/Jul/21

$${thank}\:{you} \\ $$
