Question Number 51356 by rahul 19 last updated on 26/Dec/18
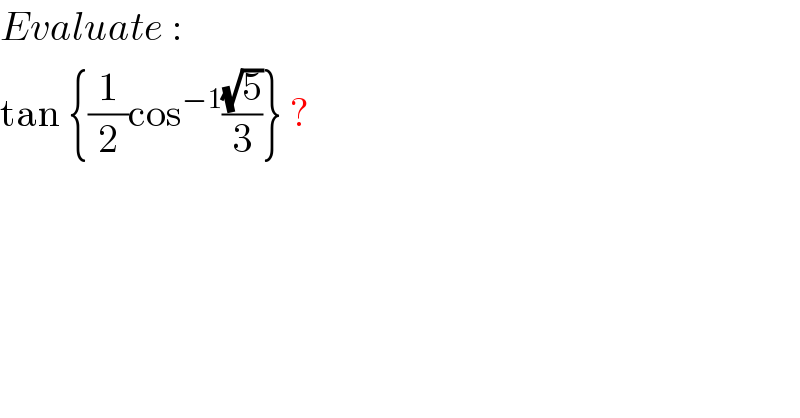
$${Evaluate}\:: \\ $$$$\mathrm{tan}\:\left\{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{−\mathrm{1}} \frac{\sqrt{\mathrm{5}}}{\mathrm{3}}\right\}\:? \\ $$
Commented by rahul 19 last updated on 26/Dec/18

$${Ans}\rightarrow\:\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{2}}. \\ $$
Answered by mr W last updated on 26/Dec/18
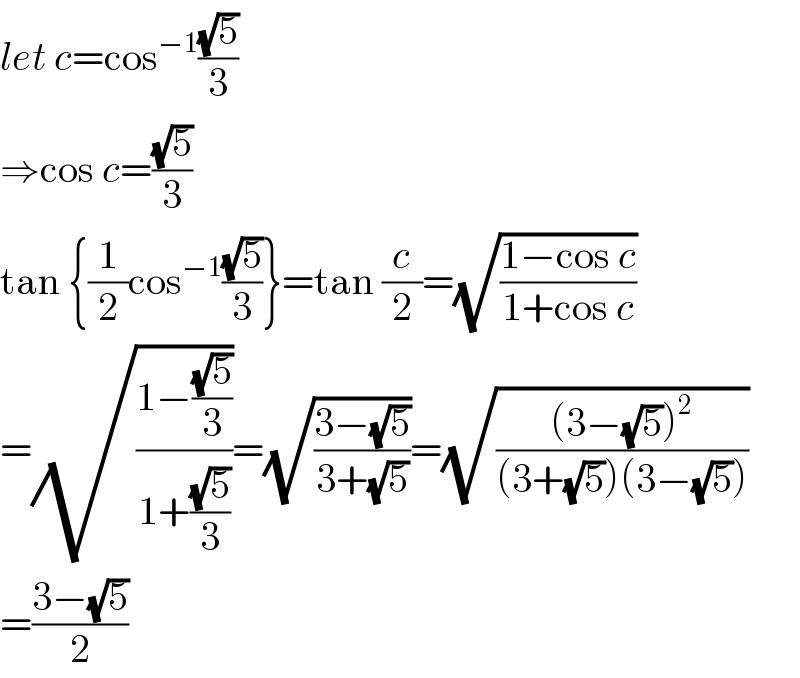
$${let}\:{c}=\mathrm{cos}^{−\mathrm{1}} \frac{\sqrt{\mathrm{5}}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{cos}\:{c}=\frac{\sqrt{\mathrm{5}}}{\mathrm{3}} \\ $$$$\mathrm{tan}\:\left\{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{−\mathrm{1}} \frac{\sqrt{\mathrm{5}}}{\mathrm{3}}\right\}=\mathrm{tan}\:\frac{{c}}{\mathrm{2}}=\sqrt{\frac{\mathrm{1}−\mathrm{cos}\:{c}}{\mathrm{1}+\mathrm{cos}\:{c}}} \\ $$$$=\sqrt{\frac{\mathrm{1}−\frac{\sqrt{\mathrm{5}}}{\mathrm{3}}}{\mathrm{1}+\frac{\sqrt{\mathrm{5}}}{\mathrm{3}}}}=\sqrt{\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{3}+\sqrt{\mathrm{5}}}}=\sqrt{\frac{\left(\mathrm{3}−\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }{\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)\left(\mathrm{3}−\sqrt{\mathrm{5}}\right)}} \\ $$$$=\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
Commented by rahul 19 last updated on 26/Dec/18
$${thank}\:{you}\:{sir}! \\ $$$${Definitely}\:{shorter}\:{than}\:{the}\:{previous} \\ $$$$\left.{one}!:\right) \\ $$
Answered by ajfour last updated on 26/Dec/18
![tan [(1/2)(2θ)]=tan [(1/2)sin^(−1) (2/3)] ⇒ sin 2θ = (2/3) = ((2t)/(1+t^2 )) ∀ t =tan θ ⇒ t^2 −3t+1 = 0 t = ((3±(√(9−4)))/2) = ((3±(√5))/2) .](https://www.tinkutara.com/question/Q51377.png)
$$\mathrm{tan}\:\left[\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\theta\right)\right]=\mathrm{tan}\:\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}}\right] \\ $$$$\Rightarrow\:\mathrm{sin}\:\mathrm{2}\theta\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:=\:\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\:\:\:\:\forall\:{t}\:=\mathrm{tan}\:\theta \\ $$$$\:\Rightarrow\:\:{t}^{\mathrm{2}} −\mathrm{3}{t}+\mathrm{1}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:{t}\:=\:\frac{\mathrm{3}\pm\sqrt{\mathrm{9}−\mathrm{4}}}{\mathrm{2}}\:=\:\frac{\mathrm{3}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\:. \\ $$
