Menu Close

Evaluate-tanx-cotx-tanx-cotx-sec-2-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 14394 by tawa tawa last updated on 31/May/17
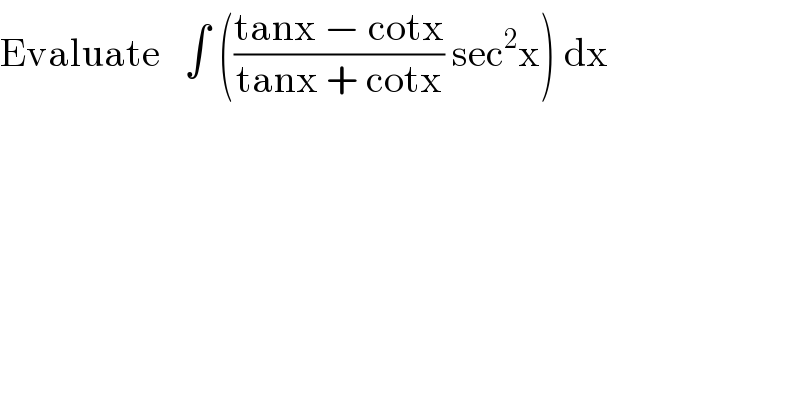
Evaluate ∫ (((tanx − cotx)/(tanx + cotx)) sec^2 x) dx
$$\mathrm{Evaluate}\:\:\:\int\:\left(\frac{\mathrm{tanx}\:−\:\mathrm{cotx}}{\mathrm{tanx}\:+\:\mathrm{cotx}}\:\mathrm{sec}^{\mathrm{2}} \mathrm{x}\right)\:\mathrm{dx} \\ $$
Answered by RasheedSindhi last updated on 31/May/17
Evaluate ∫ (((tanx − cotx)/(tanx + cotx)) sec^2 x) dx ∫ (((((sinx)/(cosx)) − ((cosx)/(sinx)))/(((sinx)/(cosx)) + ((cosx)/(sinx)))) sec^2 x) dx ∫(((sin^2 x−cos^2 x)/(sin^2 x+cos^2 x))×(1/(cos^2 x)))dx ∫(((sin^2 x−cos^2 x)/(cos^2 x)))dx ∫(tan^2 x−1)dx ∫(tan^2 x)dx−∫(1)dx ∫(sec^2 x−1)dx−x+C tanx−x−x+C tanx−2x+C
$$\mathrm{Evaluate}\:\:\:\int\:\left(\frac{\mathrm{tanx}\:−\:\mathrm{cotx}}{\mathrm{tanx}\:+\:\mathrm{cotx}}\:\mathrm{sec}^{\mathrm{2}} \mathrm{x}\right)\:\mathrm{dx} \\ $$$$\:\int\:\left(\frac{\frac{\mathrm{sinx}}{\mathrm{cosx}}\:−\:\frac{\mathrm{cosx}}{\mathrm{sinx}}}{\frac{\mathrm{sinx}}{\mathrm{cosx}}\:+\:\frac{\mathrm{cosx}}{\mathrm{sinx}}}\:\mathrm{sec}^{\mathrm{2}} \mathrm{x}\right)\:\mathrm{dx} \\ $$$$\int\left(\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}}×\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\right)\mathrm{dx} \\ $$$$\int\left(\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\right)\mathrm{dx} \\ $$$$\int\left(\mathrm{tan}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)\mathrm{dx} \\ $$$$\int\left(\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)\mathrm{dx}−\int\left(\mathrm{1}\right)\mathrm{dx} \\ $$$$\int\left(\mathrm{sec}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)\mathrm{dx}−\mathrm{x}+\mathrm{C} \\ $$$$\mathrm{tanx}−\mathrm{x}−\mathrm{x}+\mathrm{C} \\ $$$$\mathrm{tanx}−\mathrm{2x}+\mathrm{C} \\ $$$$ \\ $$
Commented by tawa tawa last updated on 31/May/17
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\: \\ $$
Commented by tawa tawa last updated on 31/May/17
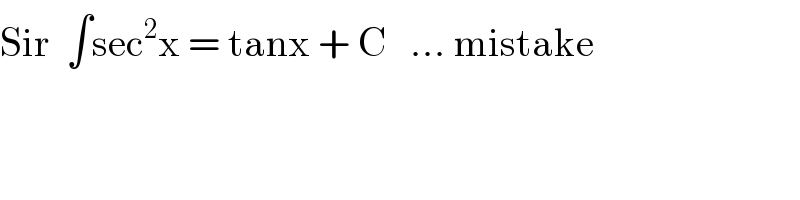
Sir ∫sec^2 x = tanx + C ... mistake
$$\mathrm{Sir}\:\:\int\mathrm{sec}^{\mathrm{2}} \mathrm{x}\:=\:\mathrm{tanx}\:+\:\mathrm{C}\:\:\:…\:\mathrm{mistake} \\ $$
Commented by RasheedSindhi last updated on 31/May/17
Mistake. Going to correct.Thanks!
$$\mathrm{Mistake}.\:\mathrm{Going}\:\mathrm{to}\:\mathrm{correct}.\mathrm{Thanks}! \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 31/May/17
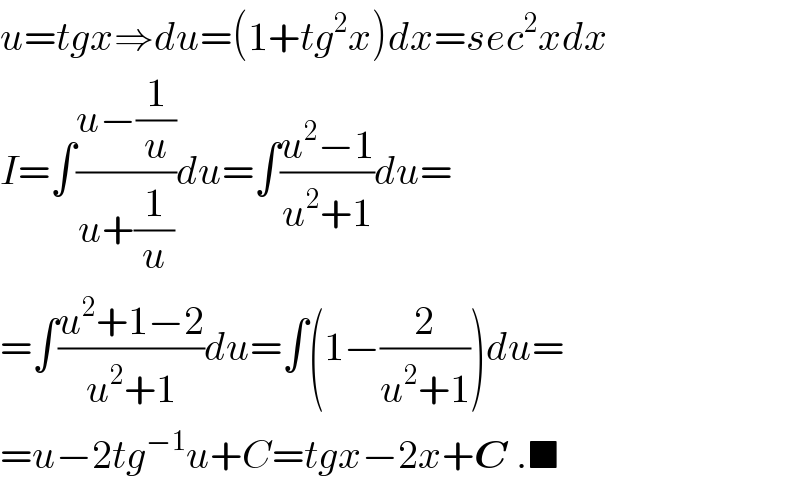
u=tgx⇒du=(1+tg^2 x)dx=sec^2 xdx I=∫((u−(1/u))/(u+(1/u)))du=∫((u^2 −1)/(u^2 +1))du= =∫((u^2 +1−2)/(u^2 +1))du=∫(1−(2/(u^2 +1)))du= =u−2tg^(−1) u+C=tgx−2x+C .■
$${u}={tgx}\Rightarrow{du}=\left(\mathrm{1}+{tg}^{\mathrm{2}} {x}\right){dx}={sec}^{\mathrm{2}} {xdx} \\ $$$${I}=\int\frac{{u}−\frac{\mathrm{1}}{{u}}}{{u}+\frac{\mathrm{1}}{{u}}}{du}=\int\frac{{u}^{\mathrm{2}} −\mathrm{1}}{{u}^{\mathrm{2}} +\mathrm{1}}{du}= \\ $$$$=\int\frac{{u}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}}{{u}^{\mathrm{2}} +\mathrm{1}}{du}=\int\left(\mathrm{1}−\frac{\mathrm{2}}{{u}^{\mathrm{2}} +\mathrm{1}}\right){du}= \\ $$$$={u}−\mathrm{2}{tg}^{−\mathrm{1}} {u}+{C}={tgx}−\mathrm{2}{x}+\boldsymbol{{C}}\:.\blacksquare \\ $$
Commented by tawa tawa last updated on 31/May/17
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *