Evaluate-the-following-by-using-integration-by-parts-formula-xsin-1-x-dx-

Question Number 163886 by zakirullah last updated on 11/Jan/22

E v a l u a t e t h e f o l l o w i n g b y u s i n g

i n t e g r a t i o n b y p a r t s f o r m u l a :

\int {x s i n}^{- 1} (x) d x

Commented by Ar Brandon last updated on 11/Jan/22

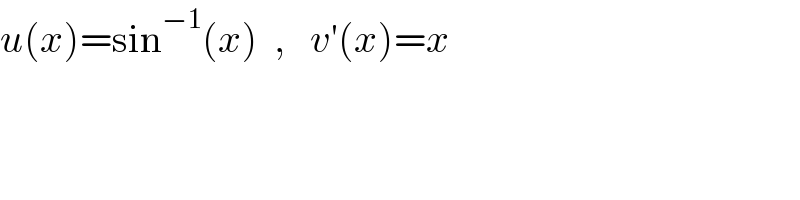
u (x) = \sin^{- 1} (x), v^{'} (x) = x

Commented by zakirullah last updated on 11/Jan/22

d e a r S i r! n e e d s o l u t i o n ?

Answered by Ar Brandon last updated on 11/Jan/22

\int x \sin^{- 1} (x) d x = \frac{1}{2} x^{2} \sin^{- 1} (x) - \frac{1}{2} \int \frac{x^{2}}{\sqrt{1 - x^{2}}} d x

= \frac{1}{2} x^{2} \sin^{- 1} (x) - \frac{1}{2} (x \sqrt{1 - x^{2}} - \int \sqrt{1 - x^{2}} d x)

\int \sqrt{1 - x^{2}} d x = \frac{1}{2} \int (1 + \cos 2 ϑ) d ϑ, x = \sin ϑ

= \frac{1}{2} (\sin^{- 1} (x) + x \sqrt{1 - x^{2}}) + C

\Rightarrow \int x \sin^{- 1} (x) d x = \frac{1}{2} x^{2} \sin^{- 1} (x) - \frac{1}{4} x \sqrt{1 - x^{2}} + \frac{1}{4} \sin^{- 1} (x) + C

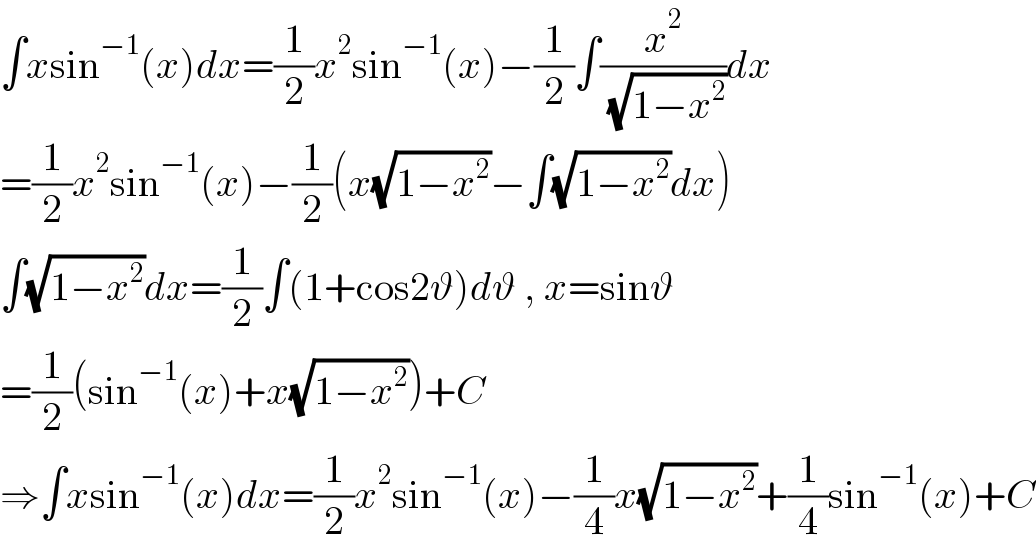
Commented by zakirullah last updated on 12/Jan/22