Menu Close

Evaluate-the-greatest-coefficient-of-7-5x-3-

Tinku Tara 0 Comments
Pin




Question Number 82149 by TawaTawa last updated on 18/Feb/20
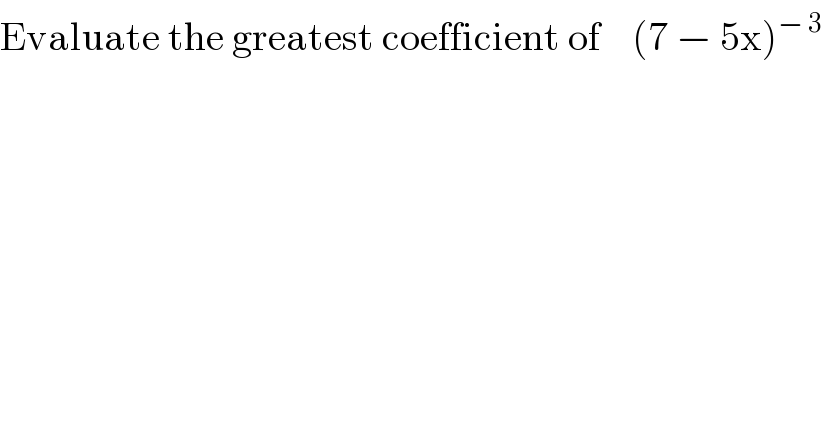
Evaluate the greatest coefficient of (7 − 5x)^(− 3)
$$\mathrm{Evaluate}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{coefficient}\:\mathrm{of}\:\:\:\:\left(\mathrm{7}\:−\:\mathrm{5x}\right)^{−\:\mathrm{3}} \\ $$
Commented by TawaTawa last updated on 18/Feb/20
Please working sir. I appreciate.
$$\mathrm{Please}\:\mathrm{working}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Answered by mr W last updated on 18/Feb/20
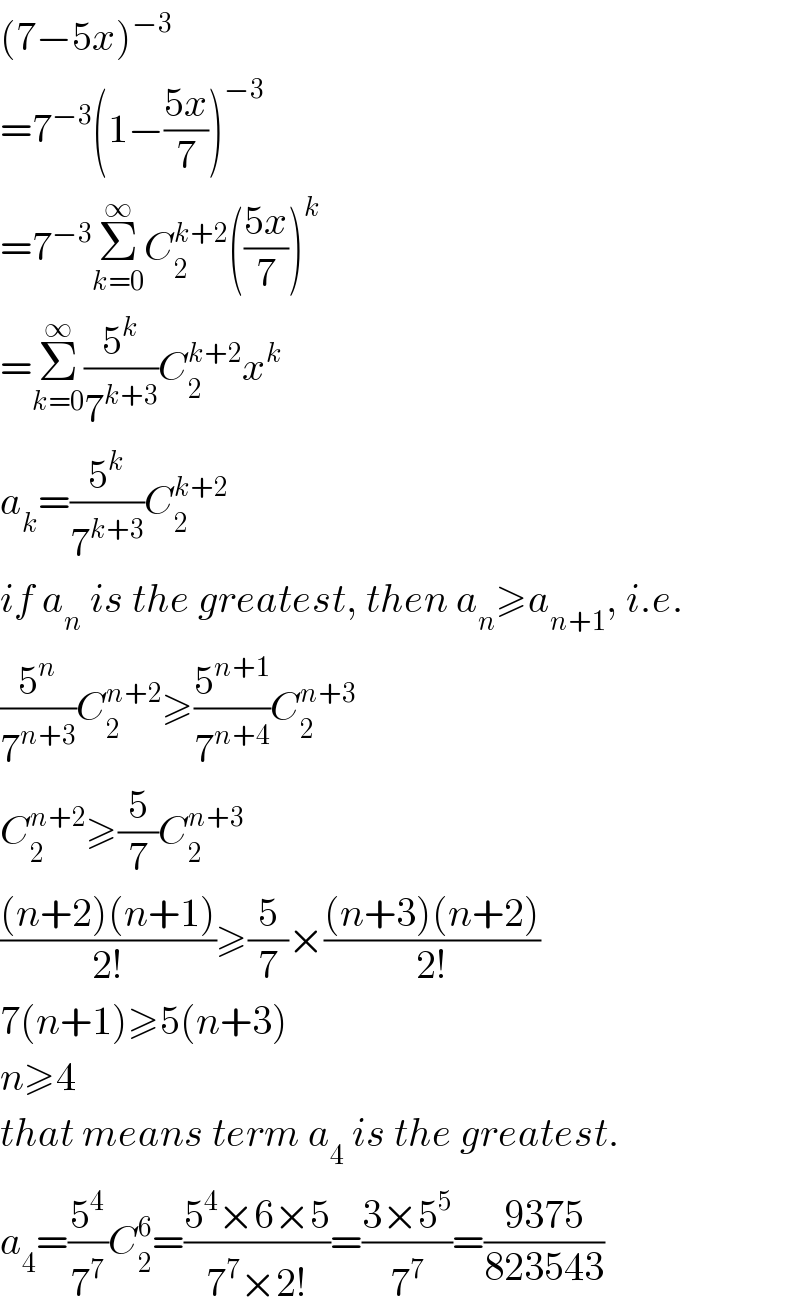
(7−5x)^(−3) =7^(−3) (1−((5x)/7))^(−3) =7^(−3) Σ_(k=0) ^∞ C_2 ^(k+2) (((5x)/7))^k =Σ_(k=0) ^∞ (5^k /7^(k+3) )C_2 ^(k+2) x^k a_k =(5^k /7^(k+3) )C_2 ^(k+2) if a_n is the greatest, then a_n ≥a_(n+1) , i.e. (5^n /7^(n+3) )C_2 ^(n+2) ≥(5^(n+1) /7^(n+4) )C_2 ^(n+3) C_2 ^(n+2) ≥(5/7)C_2 ^(n+3) (((n+2)(n+1))/(2!))≥(5/7)×(((n+3)(n+2))/(2!)) 7(n+1)≥5(n+3) n≥4 that means term a_4 is the greatest. a_4 =(5^4 /7^7 )C_2 ^6 =((5^4 ×6×5)/(7^7 ×2!))=((3×5^5 )/7^7 )=((9375)/(823543))
$$\left(\mathrm{7}−\mathrm{5}{x}\right)^{−\mathrm{3}} \\ $$$$=\mathrm{7}^{−\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{5}{x}}{\mathrm{7}}\right)^{−\mathrm{3}} \\ $$$$=\mathrm{7}^{−\mathrm{3}} \underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{\mathrm{2}} ^{{k}+\mathrm{2}} \left(\frac{\mathrm{5}{x}}{\mathrm{7}}\right)^{{k}} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{5}^{{k}} }{\mathrm{7}^{{k}+\mathrm{3}} }{C}_{\mathrm{2}} ^{{k}+\mathrm{2}} {x}^{{k}} \\ $$$${a}_{{k}} =\frac{\mathrm{5}^{{k}} }{\mathrm{7}^{{k}+\mathrm{3}} }{C}_{\mathrm{2}} ^{{k}+\mathrm{2}} \\ $$$${if}\:{a}_{{n}} \:{is}\:{the}\:{greatest},\:{then}\:{a}_{{n}} \geqslant{a}_{{n}+\mathrm{1}} ,\:{i}.{e}. \\ $$$$\frac{\mathrm{5}^{{n}} }{\mathrm{7}^{{n}+\mathrm{3}} }{C}_{\mathrm{2}} ^{{n}+\mathrm{2}} \geqslant\frac{\mathrm{5}^{{n}+\mathrm{1}} }{\mathrm{7}^{{n}+\mathrm{4}} }{C}_{\mathrm{2}} ^{{n}+\mathrm{3}} \\ $$$${C}_{\mathrm{2}} ^{{n}+\mathrm{2}} \geqslant\frac{\mathrm{5}}{\mathrm{7}}{C}_{\mathrm{2}} ^{{n}+\mathrm{3}} \\ $$$$\frac{\left({n}+\mathrm{2}\right)\left({n}+\mathrm{1}\right)}{\mathrm{2}!}\geqslant\frac{\mathrm{5}}{\mathrm{7}}×\frac{\left({n}+\mathrm{3}\right)\left({n}+\mathrm{2}\right)}{\mathrm{2}!} \\ $$$$\mathrm{7}\left({n}+\mathrm{1}\right)\geqslant\mathrm{5}\left({n}+\mathrm{3}\right) \\ $$$${n}\geqslant\mathrm{4} \\ $$$${that}\:{means}\:{term}\:{a}_{\mathrm{4}} \:{is}\:{the}\:{greatest}. \\ $$$${a}_{\mathrm{4}} =\frac{\mathrm{5}^{\mathrm{4}} }{\mathrm{7}^{\mathrm{7}} }{C}_{\mathrm{2}} ^{\mathrm{6}} =\frac{\mathrm{5}^{\mathrm{4}} ×\mathrm{6}×\mathrm{5}}{\mathrm{7}^{\mathrm{7}} ×\mathrm{2}!}=\frac{\mathrm{3}×\mathrm{5}^{\mathrm{5}} }{\mathrm{7}^{\mathrm{7}} }=\frac{\mathrm{9375}}{\mathrm{823543}} \\ $$
Commented by TawaTawa last updated on 18/Feb/20
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by mr W last updated on 19/Feb/20
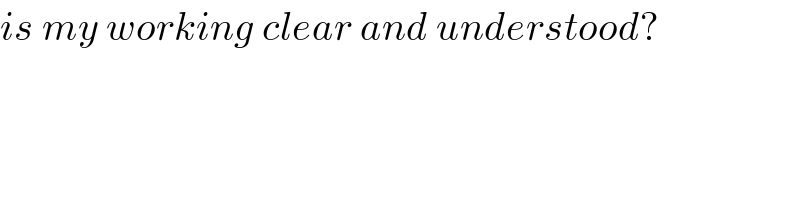
is my working clear and understood?
$${is}\:{my}\:{working}\:{clear}\:{and}\:{understood}? \\ $$
Commented by TawaTawa last updated on 19/Feb/20
It is only the third line am finding difficult to understand sir
$$\mathrm{It}\:\mathrm{is}\:\mathrm{only}\:\mathrm{the}\:\mathrm{third}\:\mathrm{line}\:\mathrm{am}\:\mathrm{finding}\:\mathrm{difficult}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{sir} \\ $$
Commented by TawaTawa last updated on 19/Feb/20
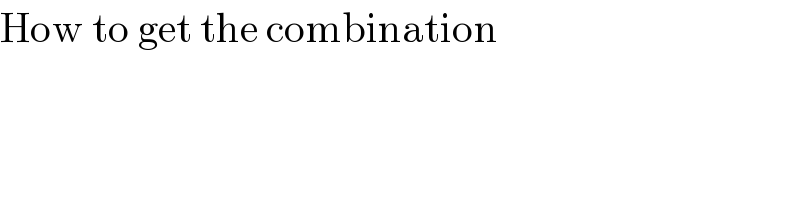
How to get the combination
$$\mathrm{How}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{combination} \\ $$
Commented by mr W last updated on 19/Feb/20
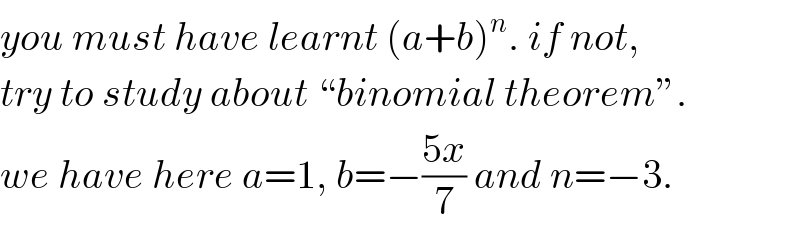
you must have learnt (a+b)^n . if not, try to study about “binomial theorem”. we have here a=1, b=−((5x)/7) and n=−3.
$${you}\:{must}\:{have}\:{learnt}\:\left({a}+{b}\right)^{{n}} .\:{if}\:{not}, \\ $$$${try}\:{to}\:{study}\:{about}\:“{binomial}\:{theorem}''. \\ $$$${we}\:{have}\:{here}\:{a}=\mathrm{1},\:{b}=−\frac{\mathrm{5}{x}}{\mathrm{7}}\:{and}\:{n}=−\mathrm{3}. \\ $$
Commented by TawaTawa last updated on 19/Feb/20
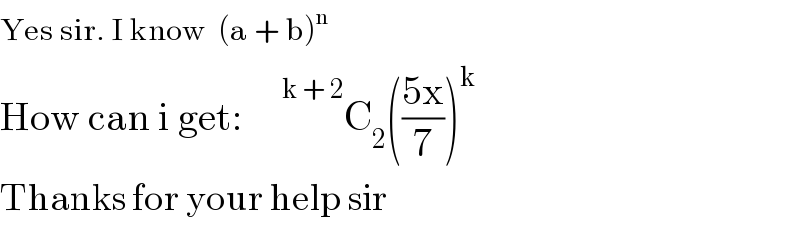
Yes sir. I know (a + b)^n How can i get: ^(k + 2) C_2 (((5x)/7))^k Thanks for your help sir
$$\mathrm{Yes}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{know}\:\:\left(\mathrm{a}\:+\:\mathrm{b}\right)^{\mathrm{n}} \\ $$$$\mathrm{How}\:\mathrm{can}\:\mathrm{i}\:\mathrm{get}:\:\:\:\:\:\overset{\mathrm{k}\:+\:\mathrm{2}} {\:}\mathrm{C}_{\mathrm{2}} \left(\frac{\mathrm{5x}}{\mathrm{7}}\right)^{\mathrm{k}} \\ $$$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{help}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 19/Feb/20
Commented by TawaTawa last updated on 19/Feb/20
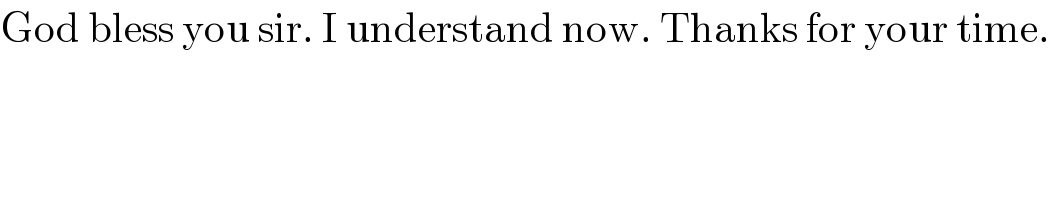
God bless you sir. I understand now. Thanks for your time.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{understand}\:\mathrm{now}.\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *