Menu Close

Evaluate-the-integral-0-1-1-x-7-1-3-1-x-3-1-7-dx-

Tinku Tara 0 Comments
Pin




Question Number 123033 by benjo_mathlover last updated on 21/Nov/20
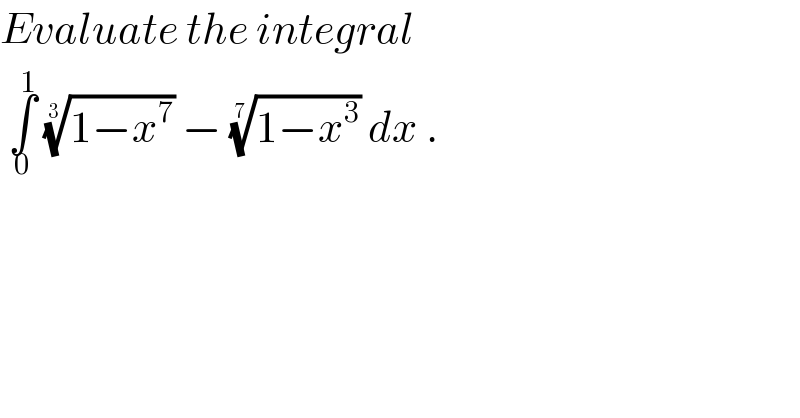
Evaluate the integral ∫_0 ^1 ((1−x^7 ))^(1/3) − ((1−x^3 ))^(1/7) dx .
$${Evaluate}\:{the}\:{integral}\: \\ $$$$\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\sqrt[{\mathrm{3}}]{\mathrm{1}−{x}^{\mathrm{7}} }\:−\:\sqrt[{\mathrm{7}}]{\mathrm{1}−{x}^{\mathrm{3}} }\:{dx}\:. \\ $$
Commented by MJS_new last updated on 22/Nov/20
answer is 0
$$\mathrm{answer}\:\mathrm{is}\:\mathrm{0} \\ $$
Answered by mathmax by abdo last updated on 22/Nov/20
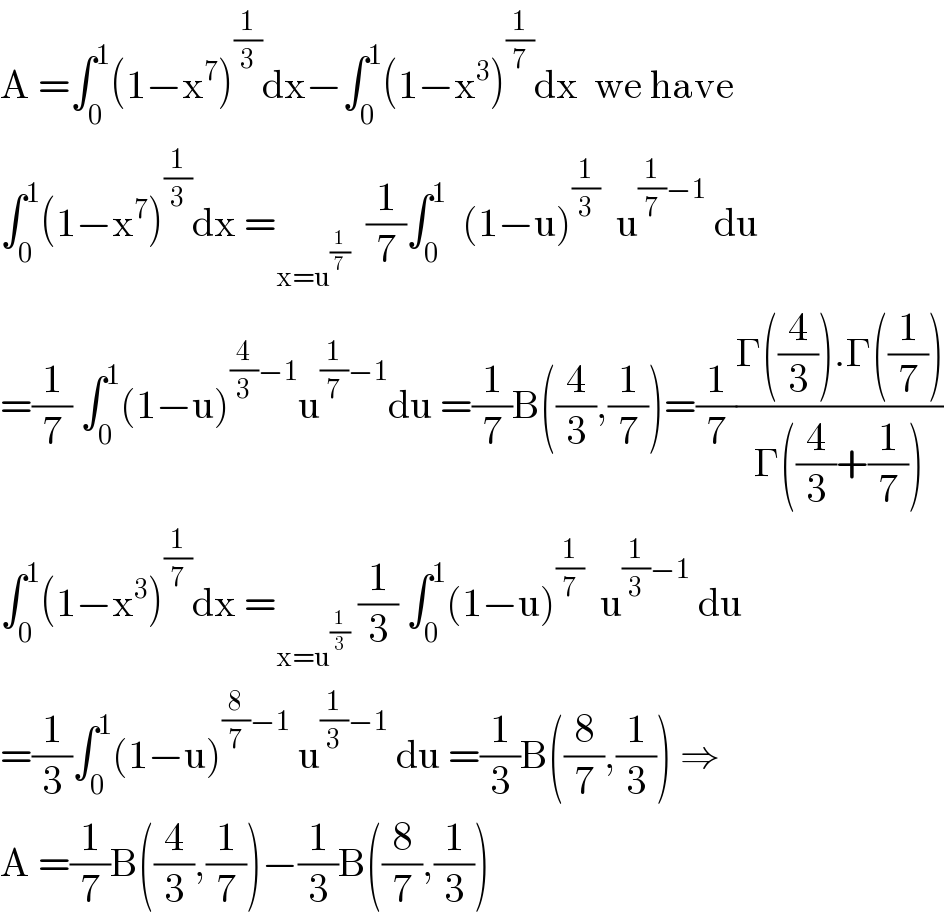
A =∫_0 ^1 (1−x^7 )^(1/3) dx−∫_0 ^1 (1−x^3 )^(1/7) dx we have ∫_0 ^1 (1−x^7 )^(1/3) dx =_(x=u^(1/7) ) (1/7)∫_0 ^1 (1−u)^(1/3) u^((1/7)−1) du =(1/7) ∫_0 ^1 (1−u)^((4/3)−1) u^((1/7)−1) du =(1/7)B((4/3),(1/7))=(1/7)((Γ((4/3)).Γ((1/7)))/(Γ((4/3)+(1/7)))) ∫_0 ^1 (1−x^3 )^(1/7) dx =_(x=u^(1/3) ) (1/3) ∫_0 ^1 (1−u)^(1/7) u^((1/3)−1) du =(1/3)∫_0 ^1 (1−u)^((8/7)−1) u^((1/3)−1) du =(1/3)B((8/7),(1/3)) ⇒ A =(1/7)B((4/3),(1/7))−(1/3)B((8/7),(1/3))
$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{7}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{7}}} \mathrm{dx}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{7}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \mathrm{dx}\:=_{\mathrm{x}=\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{7}}} } \:\:\frac{\mathrm{1}}{\mathrm{7}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\left(\mathrm{1}−\mathrm{u}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\:\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{7}}−\mathrm{1}} \:\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{7}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{u}\right)^{\frac{\mathrm{4}}{\mathrm{3}}−\mathrm{1}} \mathrm{u}^{\frac{\mathrm{1}}{\mathrm{7}}−\mathrm{1}} \mathrm{du}\:=\frac{\mathrm{1}}{\mathrm{7}}\mathrm{B}\left(\frac{\mathrm{4}}{\mathrm{3}},\frac{\mathrm{1}}{\mathrm{7}}\right)=\frac{\mathrm{1}}{\mathrm{7}}\frac{\Gamma\left(\frac{\mathrm{4}}{\mathrm{3}}\right).\Gamma\left(\frac{\mathrm{1}}{\mathrm{7}}\right)}{\Gamma\left(\frac{\mathrm{4}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{7}}\right)} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{7}}} \mathrm{dx}\:=_{\mathrm{x}=\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{3}}} } \:\frac{\mathrm{1}}{\mathrm{3}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{u}\right)^{\frac{\mathrm{1}}{\mathrm{7}}} \:\:\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} \:\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{u}\right)^{\frac{\mathrm{8}}{\mathrm{7}}−\mathrm{1}} \:\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} \:\mathrm{du}\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{B}\left(\frac{\mathrm{8}}{\mathrm{7}},\frac{\mathrm{1}}{\mathrm{3}}\right)\:\Rightarrow \\ $$$$\mathrm{A}\:=\frac{\mathrm{1}}{\mathrm{7}}\mathrm{B}\left(\frac{\mathrm{4}}{\mathrm{3}},\frac{\mathrm{1}}{\mathrm{7}}\right)−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{B}\left(\frac{\mathrm{8}}{\mathrm{7}},\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 22/Nov/20
∫_0 ^1 ((1−x^7 ))^(1/3) dx 1−x^7 =u⇒−7x^6 =(du/dx) =−(1/7)∫_1 ^0 x^(−6) u^(1/3) du =(1/7)∫_0 ^1 u^(1/3) (1−u)^(−(6/7)) du=(1/7).((Γ((4/3))Γ((1/7)))/(Γ(((31)/(21))))) And∫_0 ^1 ((1−x^3 ))^(1/7) du=(1/3).((Γ((8/7))Γ((1/3)))/(Γ(((31)/(21))))) I=(1/7).(4/3).((Γ((1/3))Γ((1/7)))/(Γ(((31)/(21))) )) −(8/(21)).((Γ((1/3))Γ((1/7)))/(Γ(((31)/(21)))))=−(4/(21)).((Γ((1/3))Γ((1/7)))/(Γ(((10)/(21))))) =−(2/5).((Γ((1/3))Γ((1/7)))/(Γ((1/3)+(1/7))))
$$\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt[{\mathrm{3}}]{\mathrm{1}−{x}^{\mathrm{7}} }\:{dx}\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}−{x}^{\mathrm{7}} ={u}\Rightarrow−\mathrm{7}{x}^{\mathrm{6}} =\frac{{du}}{{dx}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{7}}\int_{\mathrm{1}} ^{\mathrm{0}} {x}^{−\mathrm{6}} {u}^{\frac{\mathrm{1}}{\mathrm{3}}} {du}\:\:\:=\frac{\mathrm{1}}{\mathrm{7}}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{1}−{u}\right)^{−\frac{\mathrm{6}}{\mathrm{7}}} {du}=\frac{\mathrm{1}}{\mathrm{7}}.\frac{\Gamma\left(\frac{\mathrm{4}}{\mathrm{3}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{7}}\right)}{\Gamma\left(\frac{\mathrm{31}}{\mathrm{21}}\right)} \\ $$$${And}\int_{\mathrm{0}} ^{\mathrm{1}} \:\sqrt[{\mathrm{7}}]{\mathrm{1}−{x}^{\mathrm{3}} }\:{du}=\frac{\mathrm{1}}{\mathrm{3}}.\frac{\Gamma\left(\frac{\mathrm{8}}{\mathrm{7}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)}{\Gamma\left(\frac{\mathrm{31}}{\mathrm{21}}\right)} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{7}}.\frac{\mathrm{4}}{\mathrm{3}}.\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{7}}\right)}{\Gamma\left(\frac{\mathrm{31}}{\mathrm{21}}\right)\:}\:−\frac{\mathrm{8}}{\mathrm{21}}.\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{7}}\right)}{\Gamma\left(\frac{\mathrm{31}}{\mathrm{21}}\right)}=−\frac{\mathrm{4}}{\mathrm{21}}.\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{7}}\right)}{\Gamma\left(\frac{\mathrm{10}}{\mathrm{21}}\right)} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{5}}.\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{7}}\right)}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{7}}\right)} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *