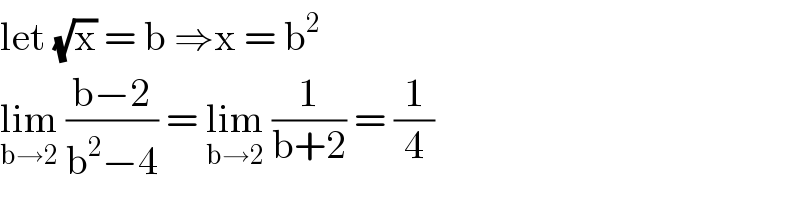Evaluate-without-using-L-hopital-s-rule-lim-x-4-x-2-x-4-

Question Number 110988 by Rio Michael last updated on 01/Sep/20

Evaluate without using L^{'} {hopital}^{'} s rule

\lim_{x \to 4} \frac{\sqrt{x} - 2}{x - 4}

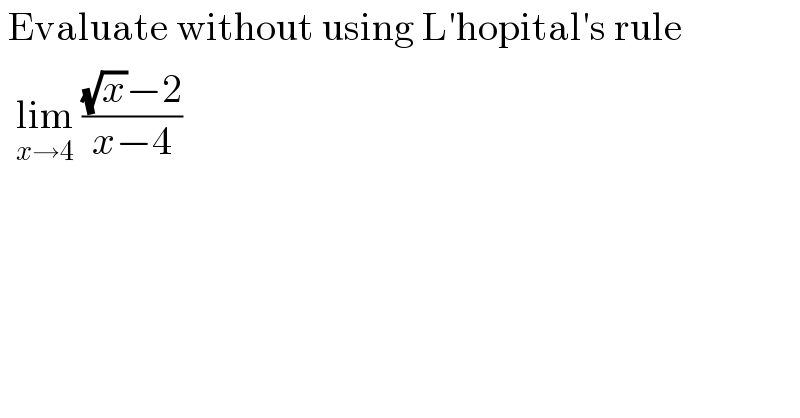
Answered by Rasheed.Sindhi last updated on 01/Sep/20

\lim_{x \to 4} \frac{\sqrt{x} - 2}{x - 4}

\frac{\sqrt{x} - 2}{{(\sqrt{x})}^{2} - {(2)}^{2}} = \frac{\sqrt{x} - 2}{(\sqrt{x} - 2) (\sqrt{x} + 2)}

= \frac{1}{(\sqrt{x} + 2)}

\lim_{x \to 4} \frac{\sqrt{x} - 2}{x - 4} = \lim_{x \to 4} \frac{1}{(\sqrt{x} + 2)} = \frac{1}{\sqrt{4} + 2}

= \frac{1}{4}

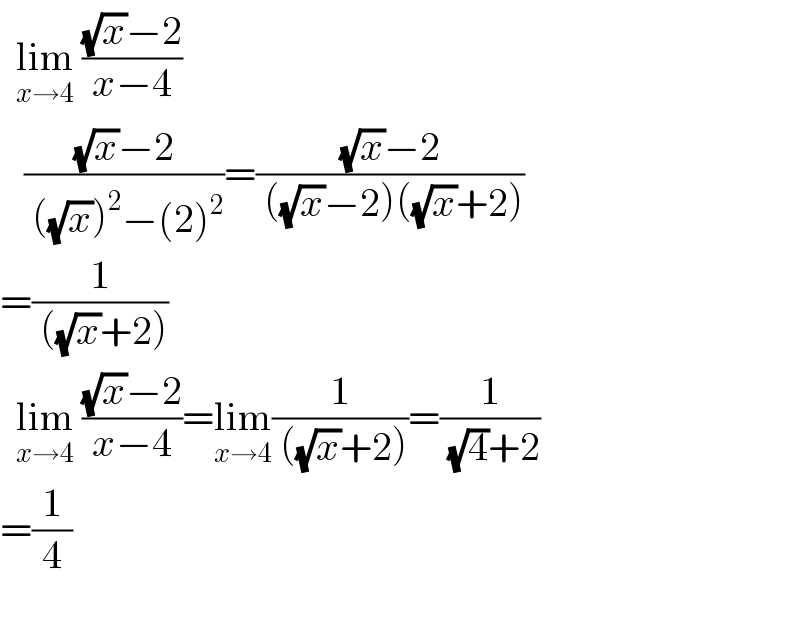
Commented by Rio Michael last updated on 01/Sep/20

correct sir .

Answered by malwan last updated on 02/Sep/20

\underset{x \to 4}{l i m} \frac{\sqrt{x} - 2}{x - 4} \times \frac{\sqrt{x} + 2}{\sqrt{x} + 2}

= \underset{x \to 4}{l i m} \frac{x - 4}{(x - 4) (\sqrt{x} + 2)}

= \underset{x \to 4}{l i m} \frac{1}{\sqrt{x} + 2} = \frac{1}{\sqrt{4} + 2} = \frac{1}{4}

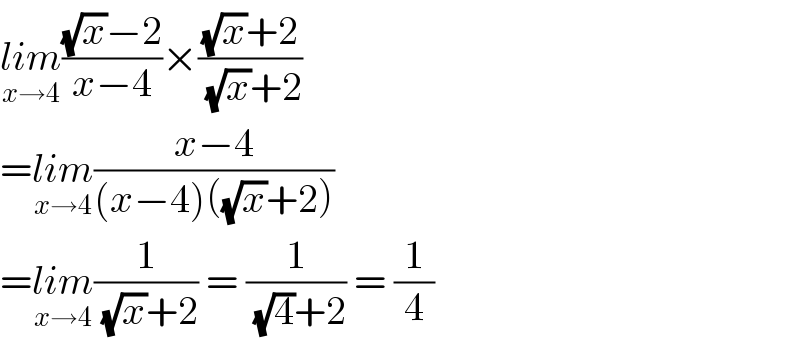
Answered by bemath last updated on 01/Sep/20

let \sqrt{x} = b \Rightarrow x = b^{2}

\lim_{b \to 2} \frac{b - 2}{b^{2} - 4} = \lim_{b \to 2} \frac{1}{b + 2} = \frac{1}{4}

Facebook Tweet Pin