Question Number 32951 by math1967 last updated on 07/Apr/18
![Evaluate ∫((x^4 +1)/(x^6 +1))dx [W.B.H.S 2018]](https://www.tinkutara.com/question/Q32951.png)
$${Evaluate} \\ $$$$\int\frac{{x}^{\mathrm{4}} +\mathrm{1}}{{x}^{\mathrm{6}} +\mathrm{1}}{dx}\:\:\:\:\:\left[{W}.{B}.{H}.{S}\:\mathrm{2018}\right] \\ $$
Commented by abdo imad last updated on 09/Apr/18

$${yes}\:{i}\:{have}\:{commited}\:{a}\:{error}\:\:{becaus}\:{i}\:{don}\:{t}\:{give}\: \\ $$$${attention}\:{to}\:{limits}\left({bornes}\right)\:{thank}\:{for}\:{this}\:{remark}… \\ $$$${i}\:{have}\:{deleted}\:{the}\:{post}.. \\ $$
Answered by Joel578 last updated on 07/Apr/18
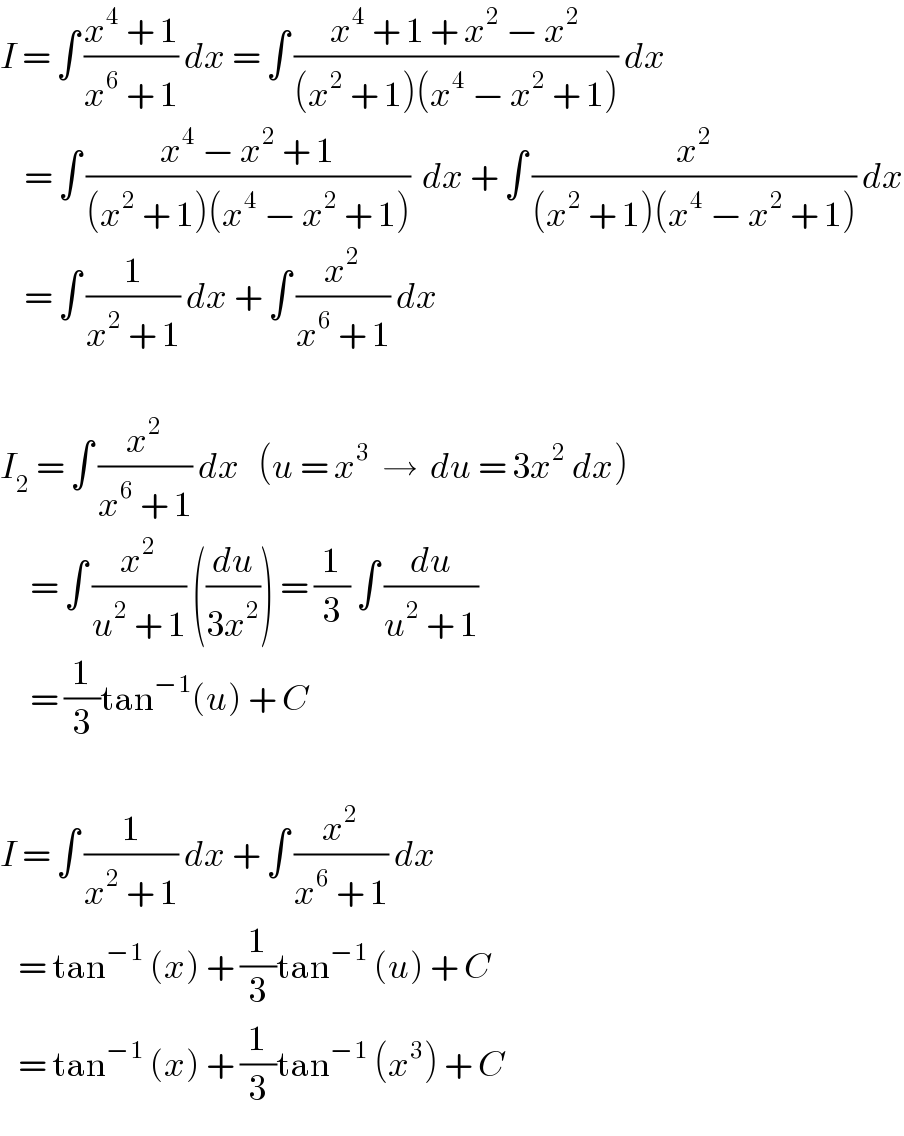
$${I}\:=\:\int\:\frac{{x}^{\mathrm{4}} \:+\:\mathrm{1}}{{x}^{\mathrm{6}} \:+\:\mathrm{1}}\:{dx}\:=\:\int\:\frac{{x}^{\mathrm{4}} \:+\:\mathrm{1}\:+\:{x}^{\mathrm{2}} \:−\:{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} \:+\:\mathrm{1}\right)\left({x}^{\mathrm{4}} \:−\:{x}^{\mathrm{2}} \:+\:\mathrm{1}\right)}\:{dx} \\ $$$$\:\:\:\:=\:\int\:\frac{{x}^{\mathrm{4}} \:−\:{x}^{\mathrm{2}} \:+\:\mathrm{1}}{\left({x}^{\mathrm{2}} \:+\:\mathrm{1}\right)\left({x}^{\mathrm{4}} \:−\:{x}^{\mathrm{2}} \:+\:\mathrm{1}\right)}\:\:{dx}\:+\:\int\:\frac{{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} \:+\:\mathrm{1}\right)\left({x}^{\mathrm{4}} \:−\:{x}^{\mathrm{2}} \:+\:\mathrm{1}\right)}\:{dx} \\ $$$$\:\:\:\:=\:\int\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:+\:\mathrm{1}}\:{dx}\:+\:\int\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{6}} \:+\:\mathrm{1}}\:{dx} \\ $$$$\: \\ $$$${I}_{\mathrm{2}} \:=\:\int\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{6}} \:+\:\mathrm{1}}\:{dx}\:\:\:\left({u}\:=\:{x}^{\mathrm{3}} \:\:\rightarrow\:\:{du}\:=\:\mathrm{3}{x}^{\mathrm{2}} \:{dx}\right) \\ $$$$\:\:\:\:\:=\:\int\:\frac{{x}^{\mathrm{2}} }{{u}^{\mathrm{2}} \:+\:\mathrm{1}}\:\left(\frac{{du}}{\mathrm{3}{x}^{\mathrm{2}} }\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\int\:\frac{{du}}{{u}^{\mathrm{2}} \:+\:\mathrm{1}} \\ $$$$\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \left({u}\right)\:+\:{C} \\ $$$$ \\ $$$${I}\:=\:\int\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:+\:\mathrm{1}}\:{dx}\:+\:\int\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{6}} \:+\:\mathrm{1}}\:{dx} \\ $$$$\:\:\:=\:\mathrm{tan}^{−\mathrm{1}} \:\left({x}\right)\:+\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \:\left({u}\right)\:+\:{C} \\ $$$$\:\:\:=\:\mathrm{tan}^{−\mathrm{1}} \:\left({x}\right)\:+\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \:\left({x}^{\mathrm{3}} \right)\:+\:{C} \\ $$
Answered by MJS last updated on 07/Apr/18
![lol! I did it the hard way... x^6 +1=(x^4 −x^2 +1)(x^2 +1)= =(x^2 −(√3)x+1)(x^2 +(√3)x+1)(x^2 +1) ((x^4 +1)/(x^6 +1))=(N_1 /(x^2 −(√3)x+1))+(N_2 /(x^2 +(√3)+1))+(N_3 /(x^2 +1 )) N_1 =N_2 =(1/6); N_3 =(2/3) ∫((x^4 +1)/(x^6 +1))dx=∫(1/(6(x^2 −(√3)x+1)))dx+∫(1/(6(x^2 +(√3)x+1)))dx+∫(2/(3(x^2 +1)))dx= [∫(1/(ax^2 +bx+c))dx=(2/( (√(−b^2 +4ac))))tan^(−1) ((2ax+b)/( (√(−b^2 +4ac)))); b^2 −4ac<0] =(1/3)(tan^(−1) (2x−(√3))+tan^(−1) (2x+(√3))+2tan^(−1) (x))+C](https://www.tinkutara.com/question/Q32957.png)
$$\mathrm{lol}!\:\mathrm{I}\:\mathrm{did}\:\mathrm{it}\:\mathrm{the}\:\mathrm{hard}\:\mathrm{way}… \\ $$$${x}^{\mathrm{6}} +\mathrm{1}=\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)= \\ $$$$=\left({x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\frac{{x}^{\mathrm{4}} +\mathrm{1}}{{x}^{\mathrm{6}} +\mathrm{1}}=\frac{{N}_{\mathrm{1}} }{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}+\frac{{N}_{\mathrm{2}} }{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}+\mathrm{1}}+\frac{{N}_{\mathrm{3}} }{{x}^{\mathrm{2}} +\mathrm{1}\:} \\ $$$${N}_{\mathrm{1}} ={N}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{6}};\:{N}_{\mathrm{3}} =\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\int\frac{{x}^{\mathrm{4}} +\mathrm{1}}{{x}^{\mathrm{6}} +\mathrm{1}}{dx}=\int\frac{\mathrm{1}}{\mathrm{6}\left({x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)}{dx}+\int\frac{\mathrm{1}}{\mathrm{6}\left({x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)}{dx}+\int\frac{\mathrm{2}}{\mathrm{3}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx}= \\ $$$$\:\:\:\:\:\left[\int\frac{\mathrm{1}}{{ax}^{\mathrm{2}} +{bx}+{c}}{dx}=\frac{\mathrm{2}}{\:\sqrt{−{b}^{\mathrm{2}} +\mathrm{4}{ac}}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}{ax}+{b}}{\:\sqrt{−{b}^{\mathrm{2}} +\mathrm{4}{ac}}};\:{b}^{\mathrm{2}} −\mathrm{4}{ac}<\mathrm{0}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{x}−\sqrt{\mathrm{3}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{x}+\sqrt{\mathrm{3}}\right)+\mathrm{2tan}^{−\mathrm{1}} \left({x}\right)\right)+{C} \\ $$
Commented by Joel578 last updated on 08/Apr/18

$$\mathrm{Great}\:\mathrm{work}\:\mathrm{Sir} \\ $$
Commented by MJS last updated on 08/Apr/18

$$\mathrm{thanks},\:\mathrm{but}\:\mathrm{I}\:\mathrm{like}\:\mathrm{your}\:\mathrm{solution} \\ $$$$\mathrm{more}\:\mathrm{than}\:\mathrm{mine} \\ $$
