Question Number 119464 by Engr_Jidda last updated on 24/Oct/20
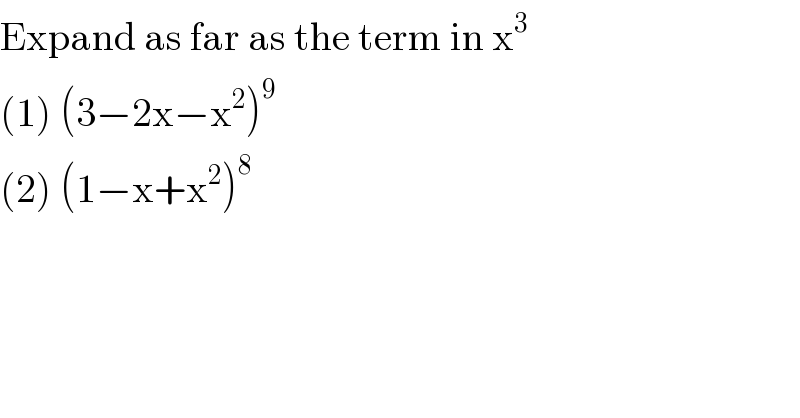
$$\mathrm{Expand}\:\mathrm{as}\:\mathrm{far}\:\mathrm{as}\:\mathrm{the}\:\mathrm{term}\:\mathrm{in}\:\mathrm{x}^{\mathrm{3}} \\ $$$$\left(\mathrm{1}\right)\:\left(\mathrm{3}−\mathrm{2x}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{9}} \\ $$$$\left(\mathrm{2}\right)\:\left(\mathrm{1}−\mathrm{x}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{8}} \\ $$
Answered by TANMAY PANACEA last updated on 24/Oct/20

$$\left.\mathrm{1}\right)\left(\mathrm{3}−\mathrm{2}{x}−{x}^{\mathrm{2}} \right)^{\mathrm{9}} \\ $$$$={a}_{\mathrm{0}} +{a}_{\mathrm{1}} {x}+{a}_{\mathrm{2}} {x}^{\mathrm{2}} +{a}_{\mathrm{3}} {x}^{\mathrm{3}} +…+{Px}^{\mathrm{18}} \\ $$$${put}\:{x}=\mathrm{0}\:{so}\:{a}_{\mathrm{0}} =\mathrm{3}^{\mathrm{9}} \\ $$$${diffdrntiate}\:{and}\:{put}\:{x}=\mathrm{0} \\ $$$$\mathrm{9}\left(\mathrm{3}−\mathrm{2}{x}−{x}^{\mathrm{2}} \right)^{\mathrm{8}} \left(−\mathrm{2}−\mathrm{2}{x}\right)=\mathrm{0}+{a}_{\mathrm{1}} +\mathrm{2}{a}_{\mathrm{2}} {x}+\mathrm{3}{a}_{\mathrm{3}} {x}^{\mathrm{2}} +..+\mathrm{18}{px}^{\mathrm{17}} \\ $$$${put}\:{x}=\mathrm{0} \\ $$$$\mathrm{9}×\mathrm{3}^{\mathrm{8}} ×\left(−\mathrm{2}\right)={a}_{\mathrm{1}} \\ $$$$\mathrm{9}\left(\mathrm{3}−\mathrm{2}{x}−{x}^{\mathrm{2}} \right)^{\mathrm{8}} \left(−\mathrm{2}\right)+\mathrm{9}×\mathrm{8}×\left(\mathrm{3}−\mathrm{2}{x}−{x}^{\mathrm{2}} \right)\left(−\mathrm{2}−\mathrm{2}{x}\right) \\ $$$$=\mathrm{0}+\mathrm{0}+\mathrm{2}{a}_{\mathrm{2}} +{terms}\:{containing}\:{x} \\ $$$${put}\:{x}=\mathrm{0} \\ $$$$\mathrm{2}{a}_{\mathrm{2}} =\mathrm{9}×\mathrm{3}^{\mathrm{8}} ×\left(−\mathrm{2}\right)+\mathrm{9}×\mathrm{8}×\left(\mathrm{3}\right)\left(−\mathrm{2}\right) \\ $$$${a}_{\mathrm{2}} =−\mathrm{9}×\mathrm{3}^{\mathrm{8}} −\mathrm{9}×\mathrm{8}×\mathrm{3} \\ $$$$\mathrm{9}×\left(−\mathrm{2}\right)×\mathrm{8}\left(\mathrm{3}−\mathrm{2}{x}−{x}^{\mathrm{2}} \right)^{\mathrm{7}} ×\left(−\mathrm{2}−\mathrm{2}{x}\right)+\mathrm{72}\left(−\mathrm{2}−\mathrm{2}{x}\right)\left(−\mathrm{2}−\mathrm{2}{x}\right)+\mathrm{72}\left(\mathrm{3}−\mathrm{2}{x}−{x}^{\mathrm{2}} \right)\left(−\mathrm{2}\right) \\ $$$$=\mathrm{0}+\mathrm{0}+\mathrm{0}+\mathrm{6}{a}_{\mathrm{3}} +{terms}\:{containing}\:{x} \\ $$$${put}\:{x}=\mathrm{0} \\ $$$$\mathrm{6}{a}_{\mathrm{3}} =\mathrm{9}×\left(−\mathrm{2}\right)×\mathrm{8}×\mathrm{3}^{\mathrm{7}} ×\left(−\mathrm{2}\right)+\mathrm{72}×\left(−\mathrm{2}\right)\left(−\mathrm{2}\right)+\mathrm{72}×\mathrm{3}×−\mathrm{2} \\ $$$${a}_{\mathrm{3}} =\mathrm{9}×\left(−\mathrm{1}\right)×\mathrm{8}×\mathrm{3}^{\mathrm{6}} ×\left(−\mathrm{2}\right)+\mathrm{12}×\mathrm{4}+\mathrm{72}×−\mathrm{1} \\ $$$$\boldsymbol{{T}}{hus}\:{wd}\:{get}\:{value}\:{a}_{\mathrm{0}} \:,\:{a}_{\mathrm{1}} ,\:\:{a}_{\mathrm{2}} ,\:{and}\:{a}_{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by TANMAY PANACEA last updated on 24/Oct/20
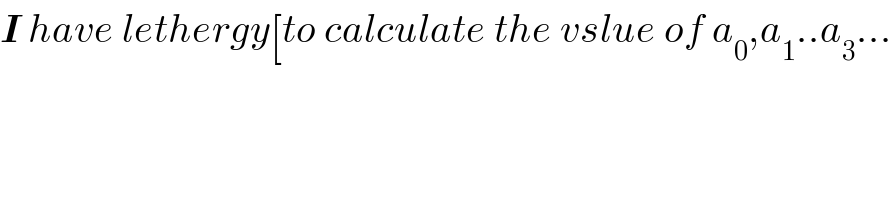
$$\boldsymbol{{I}}\:{have}\:{lethergy}\left[{to}\:{calculate}\:{the}\:{vslue}\:{of}\:{a}_{\mathrm{0}} ,{a}_{\mathrm{1}} ..{a}_{\mathrm{3}} …\right. \\ $$
Commented by Engr_Jidda last updated on 24/Oct/20
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir} \\ $$
Answered by TANMAY PANACEA last updated on 24/Oct/20
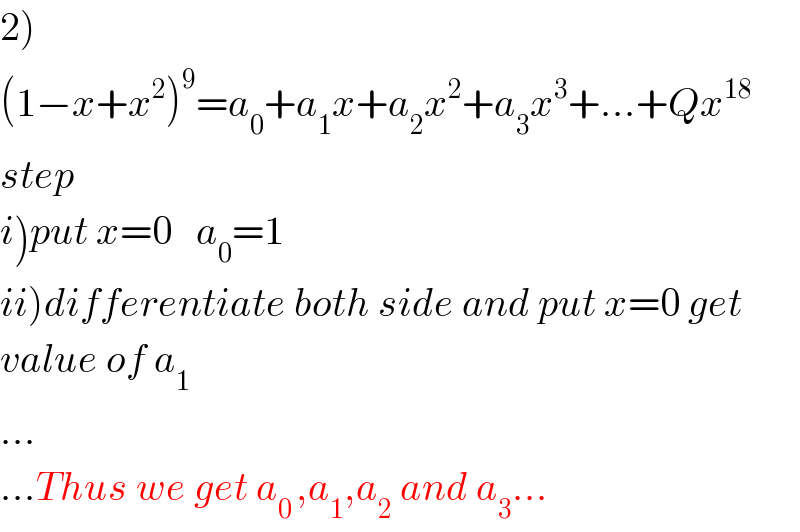
$$\left.\mathrm{2}\right) \\ $$$$\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)^{\mathrm{9}} ={a}_{\mathrm{0}} +{a}_{\mathrm{1}} {x}+{a}_{\mathrm{2}} {x}^{\mathrm{2}} +{a}_{\mathrm{3}} {x}^{\mathrm{3}} +…+{Qx}^{\mathrm{18}} \\ $$$${step}\: \\ $$$$\left.{i}\right){put}\:{x}=\mathrm{0}\:\:\:{a}_{\mathrm{0}} =\mathrm{1} \\ $$$$\left.{ii}\right){differentiate}\:{both}\:{side}\:{and}\:{put}\:{x}=\mathrm{0}\:{get} \\ $$$${value}\:{of}\:{a}_{\mathrm{1}} \\ $$$$… \\ $$$$…{Thus}\:{we}\:{get}\:{a}_{\mathrm{0}\:} ,{a}_{\mathrm{1}} ,{a}_{\mathrm{2}} \:{and}\:{a}_{\mathrm{3}} … \\ $$
Commented by Engr_Jidda last updated on 24/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by TANMAY PANACEA last updated on 24/Oct/20
$${most}\:{welcome}\:{sir} \\ $$
