Question Number 107883 by Ar Brandon last updated on 13/Aug/20
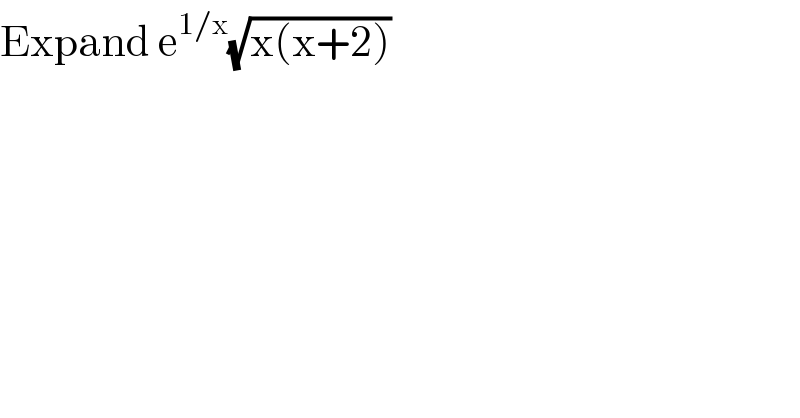
$$\mathrm{Expand}\:\mathrm{e}^{\mathrm{1}/\mathrm{x}} \sqrt{\mathrm{x}\left(\mathrm{x}+\mathrm{2}\right)} \\ $$
Answered by Dwaipayan Shikari last updated on 13/Aug/20
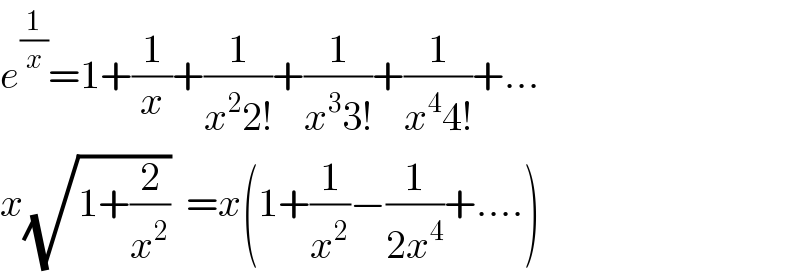
$${e}^{\frac{\mathrm{1}}{{x}}} =\mathrm{1}+\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} \mathrm{2}!}+\frac{\mathrm{1}}{{x}^{\mathrm{3}} \mathrm{3}!}+\frac{\mathrm{1}}{{x}^{\mathrm{4}} \mathrm{4}!}+… \\ $$$${x}\sqrt{\mathrm{1}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} }}\:\:={x}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{4}} }+….\right) \\ $$
