Question Number 113630 by mathmax by abdo last updated on 14/Sep/20
$$\mathrm{explicit}\:\mathrm{g}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{acos}^{\mathrm{2}} \theta\right)\mathrm{d}\theta \\ $$
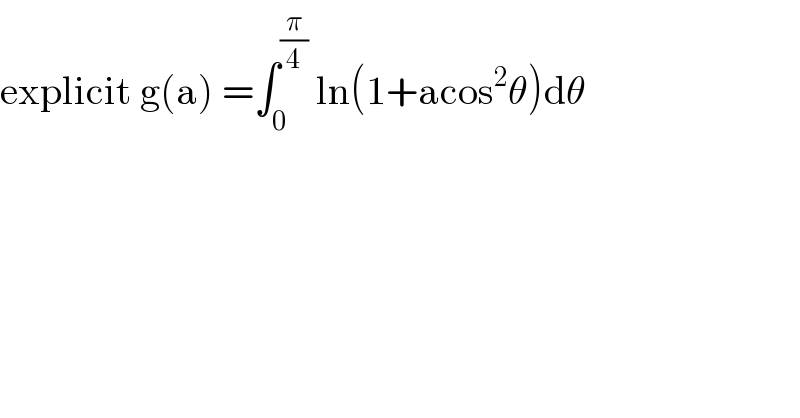
Answered by Dwaipayan Shikari last updated on 15/Sep/20
![I(a)=∫_0 ^(π/4) log(1+acos^2 θ)dθ I′(a)=∫_0 ^(π/4) ((cos^2 θ)/(1+acos^2 θ)) I′(a)=(1/a)∫_0 ^(π/4) 1−(1/(1+acos^2 θ)) I^′ (a)=(π/(4a))−∫^(π/4) ((sec^2 θ)/(sec^2 θ+a))dθ I′(a)=(π/(4a))−∫_0 ^(π/4) ((sec^2 θ)/(tan^2 θ+1+a)) I′(a)=(π/(4a))−∫_0 ^1 (dt/(t^2 +((√(1+a)))^2 )) I′(a)=(π/(4a))−[(1/( (√(1+a))))tan^(−1) (t/( (√(1+a))))]_0 ^1 I(a)=∫(π/(4a))−∫(1/( (√(1+a))))tan^(−1) (1/( (√(1+a))))da I(a)=(π/4)log(a)−∫((2u)/u).tan^(−1) (1/u)du 1+a=u^2 ,1=2u(du/da) I(a)=(π/4)log(a)−2∫tan^(−1) (1/u)du tan^(−1) (1/u)=α I(a)=(π/4)log(a)−2utan^(−1) (1/u)−2∫(1/( u(√(1+(1/u^2 )))))du I(a)=(π/4)log(a)−2(√(1+a)) tan^(−1) (1/( (√(1+a))))−2log(u+(√(u^2 +1)))+C I(a)=(π/4)log(a)−2(√(1+a)) tan^(−1) (1/( (√(1+a))))−2log((√(1+a))+(√(2+a)))+C I(−1)=(π^2 /4)i+C=∫_0 ^(π/4) log(1−cos^2 x)dx ∫_0 ^(π/4) log(1−cos^2 x)dx=∫_(−(π/2)) ^(π/2) log(sinx)dx=∫_0 ^(π/2) log(sinx)+∫_(−(π/2)) ^0 log(sinx) =−(π/2)log(2)+∫_(−(π/2)) ^0 log(−1)+log(cosx)=(π^2 /2)i I(−1)=(π^2 /4)i+C=((π^2 i)/2)⇒C=(π^2 /4)i I(a)=(π/4)log(a)−2(√(1+a)) tan^(−1) (1/( (√(1+a))))−2log((√(1+a))+(√(2+a)))+(π^2 /4)i](https://www.tinkutara.com/question/Q113639.png)
$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\left(\mathrm{1}+{acos}^{\mathrm{2}} \theta\right){d}\theta \\ $$$${I}'\left({a}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{cos}^{\mathrm{2}} \theta}{\mathrm{1}+{acos}^{\mathrm{2}} \theta} \\ $$$${I}'\left({a}\right)=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{acos}^{\mathrm{2}} \theta} \\ $$$${I}^{'} \left({a}\right)=\frac{\pi}{\mathrm{4}{a}}−\int^{\frac{\pi}{\mathrm{4}}} \frac{{sec}^{\mathrm{2}} \theta}{{sec}^{\mathrm{2}} \theta+{a}}{d}\theta \\ $$$${I}'\left({a}\right)=\frac{\pi}{\mathrm{4}{a}}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{sec}^{\mathrm{2}} \theta}{{tan}^{\mathrm{2}} \theta+\mathrm{1}+{a}} \\ $$$${I}'\left({a}\right)=\frac{\pi}{\mathrm{4}{a}}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{{t}^{\mathrm{2}} +\left(\sqrt{\mathrm{1}+{a}}\right)^{\mathrm{2}} } \\ $$$${I}'\left({a}\right)=\frac{\pi}{\mathrm{4}{a}}−\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}}{tan}^{−\mathrm{1}} \frac{{t}}{\:\sqrt{\mathrm{1}+{a}}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$${I}\left({a}\right)=\int\frac{\pi}{\mathrm{4}{a}}−\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}}{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}}{da} \\ $$$${I}\left({a}\right)=\frac{\pi}{\mathrm{4}}{log}\left({a}\right)−\int\frac{\mathrm{2}{u}}{{u}}.{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{u}}{du}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}+{a}={u}^{\mathrm{2}} ,\mathrm{1}=\mathrm{2}{u}\frac{{du}}{{da}} \\ $$$${I}\left({a}\right)=\frac{\pi}{\mathrm{4}}{log}\left({a}\right)−\mathrm{2}\int{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{u}}{du}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{u}}=\alpha \\ $$$${I}\left({a}\right)=\frac{\pi}{\mathrm{4}}{log}\left({a}\right)−\mathrm{2}{utan}^{−\mathrm{1}} \frac{\mathrm{1}}{{u}}−\mathrm{2}\int\frac{\mathrm{1}}{\:{u}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{u}^{\mathrm{2}} }}}{du} \\ $$$${I}\left({a}\right)=\frac{\pi}{\mathrm{4}}{log}\left({a}\right)−\mathrm{2}\sqrt{\mathrm{1}+{a}}\:{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}}−\mathrm{2}{log}\left({u}+\sqrt{{u}^{\mathrm{2}} +\mathrm{1}}\right)+{C} \\ $$$${I}\left({a}\right)=\frac{\pi}{\mathrm{4}}{log}\left({a}\right)−\mathrm{2}\sqrt{\mathrm{1}+{a}}\:{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}}−\mathrm{2}{log}\left(\sqrt{\mathrm{1}+{a}}+\sqrt{\mathrm{2}+{a}}\right)+{C} \\ $$$${I}\left(−\mathrm{1}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}{i}+{C}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right){dx}=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sinx}\right){dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sinx}\right)+\int_{−\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} {log}\left({sinx}\right) \\ $$$$=−\frac{\pi}{\mathrm{2}}{log}\left(\mathrm{2}\right)+\int_{−\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} {log}\left(−\mathrm{1}\right)+{log}\left({cosx}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}{i} \\ $$$${I}\left(−\mathrm{1}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}{i}+{C}=\frac{\pi^{\mathrm{2}} {i}}{\mathrm{2}}\Rightarrow{C}=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}{i} \\ $$$${I}\left({a}\right)=\frac{\pi}{\mathrm{4}}{log}\left({a}\right)−\mathrm{2}\sqrt{\mathrm{1}+{a}}\:{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}}}−\mathrm{2}{log}\left(\sqrt{\mathrm{1}+{a}}+\sqrt{\mathrm{2}+{a}}\right)+\frac{\pi^{\mathrm{2}} }{\mathrm{4}}{i} \\ $$
Commented by Tawa11 last updated on 06/Sep/21
$$\mathrm{great}\:\mathrm{sir} \\ $$
Answered by mathmax by abdo last updated on 14/Sep/20
$$\mid\mathrm{a}\mid<\mathrm{1} \\ $$
Answered by Olaf last updated on 14/Sep/20
![(1/(1+acos^2 θ)) = Σ_(k=0) ^∞ (−1)^k a^k cos^(2k) θ −((2acosθsinθ)/(1+acos^2 θ)) = −2asinθcosθΣ_(k=0) ^∞ (−1)^k a^k cos^(2k) θ −((2acosθsinθ)/(1+acos^2 θ)) = −2asinθΣ_(k=0) ^∞ (−1)^k a^k cos^(2k+1) θ ln(1+acos^2 θ) = −2aΣ_(k=0) ^∞ (−1)^k a^k ((cos^(2k+2) θ)/(2k+2)) ∫_0 ^(π/4) ln(1+acos^2 θ)dθ = −2aΣ_(k=0) ^∞ (((−1)^k a^k )/(2k+2))∫_0 ^(π/4) cos^(2k+2) θdθ cos^(2k) θ = (((1+cos2θ)/2))^k cos^(2k) θ = (1/2^k )Σ_(p=0) ^k C_k ^p cos^p 2θ ∫_0 ^(π/4) ln(1+acos^2 θ)dθ = −2aΣ_(k=0) ^∞ (((−1)^k a^k )/(2k+2))[((cos^2 θ)/2^k )Σ_(p=0) ^k C_k ^p cos^p 2θ]_0 ^(π/4) ∫_0 ^(π/4) ln(1+acos^2 θ)dθ = 2aΣ_(k=0) ^∞ (((−1)^k a^k )/((2k+2)2^k ))Σ_(p=0) ^k C_k ^p ∫_0 ^(π/4) ln(1+acos^2 θ)dθ = 2aΣ_(k=0) ^∞ (((−1)^k a^k )/((2k+2))) ...](https://www.tinkutara.com/question/Q113702.png)
$$\frac{\mathrm{1}}{\mathrm{1}+{a}\mathrm{cos}^{\mathrm{2}} \theta}\:=\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} \mathrm{cos}^{\mathrm{2}{k}} \theta \\ $$$$−\frac{\mathrm{2}{a}\mathrm{cos}\theta\mathrm{sin}\theta}{\mathrm{1}+{a}\mathrm{cos}^{\mathrm{2}} \theta}\:=\:−\mathrm{2}{a}\mathrm{sin}\theta\mathrm{cos}\theta\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} \mathrm{cos}^{\mathrm{2}{k}} \theta \\ $$$$−\frac{\mathrm{2}{a}\mathrm{cos}\theta\mathrm{sin}\theta}{\mathrm{1}+{a}\mathrm{cos}^{\mathrm{2}} \theta}\:=\:−\mathrm{2}{a}\mathrm{sin}\theta\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} \mathrm{cos}^{\mathrm{2}{k}+\mathrm{1}} \theta \\ $$$$\mathrm{ln}\left(\mathrm{1}+{a}\mathrm{cos}^{\mathrm{2}} \theta\right)\:=\:−\mathrm{2}{a}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} \frac{\mathrm{cos}^{\mathrm{2}{k}+\mathrm{2}} \theta}{\mathrm{2}{k}+\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+{a}\mathrm{cos}^{\mathrm{2}} \theta\right){d}\theta\:=\:−\mathrm{2}{a}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} }{\mathrm{2}{k}+\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{cos}^{\mathrm{2}{k}+\mathrm{2}} \theta{d}\theta \\ $$$$\mathrm{cos}^{\mathrm{2}{k}} \theta\:=\:\left(\frac{\mathrm{1}+\mathrm{cos2}\theta}{\mathrm{2}}\right)^{{k}} \\ $$$$\mathrm{cos}^{\mathrm{2}{k}} \theta\:=\:\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\underset{{p}=\mathrm{0}} {\overset{{k}} {\sum}}\mathrm{C}_{{k}} ^{{p}} \mathrm{cos}^{{p}} \mathrm{2}\theta \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+{a}\mathrm{cos}^{\mathrm{2}} \theta\right){d}\theta\:=\:−\mathrm{2}{a}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} }{\mathrm{2}{k}+\mathrm{2}}\left[\frac{\mathrm{cos}^{\mathrm{2}} \theta}{\mathrm{2}^{{k}} }\underset{{p}=\mathrm{0}} {\overset{{k}} {\sum}}\mathrm{C}_{{k}} ^{{p}} \mathrm{cos}^{{p}} \mathrm{2}\theta\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+{a}\mathrm{cos}^{\mathrm{2}} \theta\right){d}\theta\:=\:\mathrm{2}{a}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} }{\left(\mathrm{2}{k}+\mathrm{2}\right)\mathrm{2}^{{k}} }\underset{{p}=\mathrm{0}} {\overset{{k}} {\sum}}\mathrm{C}_{{k}} ^{{p}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+{a}\mathrm{cos}^{\mathrm{2}} \theta\right){d}\theta\:=\:\mathrm{2}{a}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} }{\left(\mathrm{2}{k}+\mathrm{2}\right)} \\ $$$$… \\ $$