Menu Close

explicite-f-a-0-lnx-x-2-x-a-dx-with-a-gt-1-4-

Tinku Tara 0 Comments
Pin




Question Number 127777 by Bird last updated on 02/Jan/21
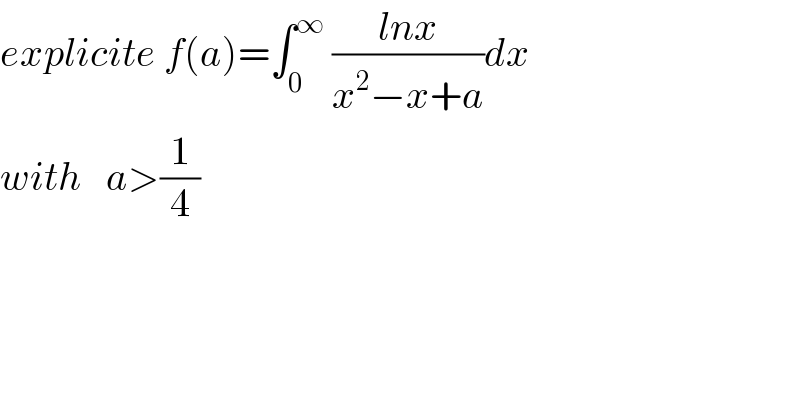
explicite f(a)=∫_0 ^∞ ((lnx)/(x^2 −x+a))dx with a>(1/4)
$${explicite}\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{{lnx}}{{x}^{\mathrm{2}} −{x}+{a}}{dx} \\ $$$${with}\:\:\:{a}>\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Answered by mathmax by abdo last updated on 03/Jan/21
let f(z)=((ln^2 z)/(z^2 −z+a)) we have f(a)=−(1/2)Re(Σ Res(f,z_i )) poles of f →Δ=1−4a<0 ⇒z_1 =((1+i(√(4a−1)))/2) and z_2 =((1−i(√(4a−1)))/2) we have ∣z_1 ∣=(1/2)(√(1+4a−1)))=(√a) ⇒ z_1 =(√a)e^(iarctan(√(4a−1))) and z_2 =(√a)e^(−iarctan(√(4a−1))) f(z)=((ln^2 z)/((z−z_1 )(z−z_2 ))) Res(f,z_1 )=((ln^2 z_1 )/(z_1 −z_2 )) =(((ln(√a)+iarctan(√(4a))−1)^2 )/(i(√(4a−1)))) =((ln^2 ((√a))+2iln(√a)arctan(√(4a−1))−arctan^2 (√(4a−1)))/(i(√(4a−1)))) Res(f,z_2 )=((ln^2 z_2 )/(z_2 −z_1 )) =(((ln(√a)−iarctan(√(4a−1)))^2 )/(−i(√(4a−1)))) =((ln^2 (√a)−2iln(√a)arctan(√(4a−1))−arctan^2 (√(4a−1)))/(−i(√(4a−1)))) ⇒ Σ Res(f)=(1/(i(√(4a−1)))){ln^2 ((√a))+2iln(√a)arctan(√(4a−1))−arctan^2 (√(4a−1)) −ln^2 (√a)+2iln(√a)arctan(√(4a−1))+arctan^2 (√(4a−1))} =(1/(i(√(4a−1))))(2iln((√a))arctan(√(4a−1)))=((lna)/( (√(4a−1)))) arctan(√(4a−1)) ⇒ f(a) =−((lna)/(2(√(4a−1)))) arctan(√(4a−1))
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{a}}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{a}\right)=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left(\Sigma\:\mathrm{Res}\left(\mathrm{f},\mathrm{z}_{\mathrm{i}} \right)\right) \\ $$$$\mathrm{poles}\:\mathrm{of}\:\mathrm{f}\:\:\:\:\rightarrow\Delta=\mathrm{1}−\mathrm{4a}<\mathrm{0}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{\mathrm{1}+\mathrm{i}\sqrt{\mathrm{4a}−\mathrm{1}}}{\mathrm{2}} \\ $$$$\left.\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\frac{\mathrm{1}−\mathrm{i}\sqrt{\mathrm{4a}−\mathrm{1}}}{\mathrm{2}}\:\:\mathrm{we}\:\mathrm{have}\:\mid\mathrm{z}_{\mathrm{1}} \mid=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{1}+\mathrm{4a}−\mathrm{1}}\right)=\sqrt{\mathrm{a}}\:\Rightarrow \\ $$$$\mathrm{z}_{\mathrm{1}} =\sqrt{\mathrm{a}}\mathrm{e}^{\mathrm{iarctan}\sqrt{\mathrm{4a}−\mathrm{1}}} \:\:\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\sqrt{\mathrm{a}}\mathrm{e}^{−\mathrm{iarctan}\sqrt{\mathrm{4a}−\mathrm{1}}} \\ $$$$\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)} \\ $$$$\mathrm{Res}\left(\mathrm{f},\mathrm{z}_{\mathrm{1}} \right)=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}_{\mathrm{1}} }{\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} }\:=\frac{\left(\mathrm{ln}\sqrt{\mathrm{a}}+\mathrm{iarctan}\sqrt{\mathrm{4a}}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{i}\sqrt{\mathrm{4a}−\mathrm{1}}} \\ $$$$=\frac{\mathrm{ln}^{\mathrm{2}} \left(\sqrt{\mathrm{a}}\right)+\mathrm{2iln}\sqrt{\mathrm{a}}\mathrm{arctan}\sqrt{\mathrm{4a}−\mathrm{1}}−\mathrm{arctan}^{\mathrm{2}} \sqrt{\mathrm{4a}−\mathrm{1}}}{\mathrm{i}\sqrt{\mathrm{4a}−\mathrm{1}}} \\ $$$$\mathrm{Res}\left(\mathrm{f},\mathrm{z}_{\mathrm{2}} \right)=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}_{\mathrm{2}} }{\mathrm{z}_{\mathrm{2}} −\mathrm{z}_{\mathrm{1}} }\:=\frac{\left(\mathrm{ln}\sqrt{\mathrm{a}}−\mathrm{iarctan}\sqrt{\mathrm{4a}−\mathrm{1}}\right)^{\mathrm{2}} }{−\mathrm{i}\sqrt{\mathrm{4a}−\mathrm{1}}} \\ $$$$=\frac{\mathrm{ln}^{\mathrm{2}} \sqrt{\mathrm{a}}−\mathrm{2iln}\sqrt{\mathrm{a}}\mathrm{arctan}\sqrt{\mathrm{4a}−\mathrm{1}}−\mathrm{arctan}^{\mathrm{2}} \sqrt{\mathrm{4a}−\mathrm{1}}}{−\mathrm{i}\sqrt{\mathrm{4a}−\mathrm{1}}}\:\Rightarrow \\ $$$$\Sigma\:\mathrm{Res}\left(\mathrm{f}\right)=\frac{\mathrm{1}}{\mathrm{i}\sqrt{\mathrm{4a}−\mathrm{1}}}\left\{\mathrm{ln}^{\mathrm{2}} \left(\sqrt{\mathrm{a}}\right)+\mathrm{2iln}\sqrt{\mathrm{a}}\mathrm{arctan}\sqrt{\mathrm{4a}−\mathrm{1}}−\mathrm{arctan}^{\mathrm{2}} \sqrt{\mathrm{4a}−\mathrm{1}}\right. \\ $$$$\left.−\mathrm{ln}^{\mathrm{2}} \sqrt{\mathrm{a}}+\mathrm{2iln}\sqrt{\mathrm{a}}\mathrm{arctan}\sqrt{\mathrm{4a}−\mathrm{1}}+\mathrm{arctan}^{\mathrm{2}} \sqrt{\mathrm{4a}−\mathrm{1}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{i}\sqrt{\mathrm{4a}−\mathrm{1}}}\left(\mathrm{2iln}\left(\sqrt{\mathrm{a}}\right)\mathrm{arctan}\sqrt{\mathrm{4a}−\mathrm{1}}\right)=\frac{\mathrm{lna}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\:\mathrm{arctan}\sqrt{\mathrm{4a}−\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=−\frac{\mathrm{lna}}{\mathrm{2}\sqrt{\mathrm{4a}−\mathrm{1}}}\:\mathrm{arctan}\sqrt{\mathrm{4a}−\mathrm{1}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *