Question Number 167510 by Mathspace last updated on 18/Mar/22
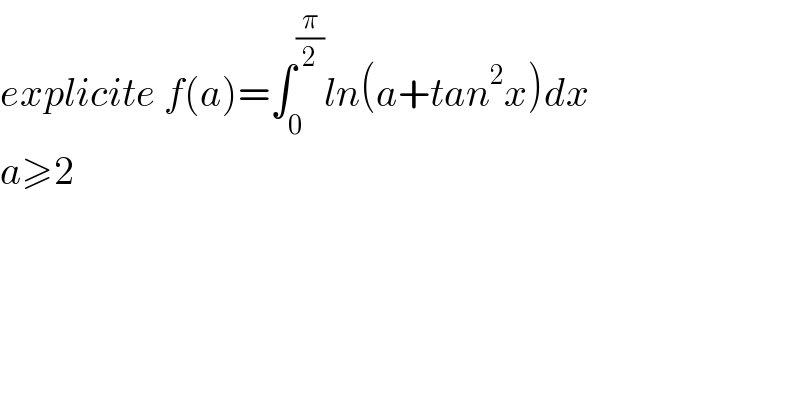
$${explicite}\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({a}+{tan}^{\mathrm{2}} {x}\right){dx} \\ $$$${a}\geqslant\mathrm{2} \\ $$
Answered by ArielVyny last updated on 20/Mar/22
![f(a)=∫_0 ^(π/2) ln(a+tan^2 x)dx f′(a)=∫_0 ^(π/2) (1/(a+tan^2 x))dx t=tanx→dt=(1+t^2 )dx ∫_0 ^1 (1/(a+t^2 )).(1/(1+t^2 ))dt=∫_0 ^1 (1/(a+t^2 )).[1−(t^2 /(1+t^2 ))]dt (1/a)∫_0 ^1 (1/(1+((t/( (√a))))^2 ))dt−∫_0 ^1 (t^2 /((1+t^2 )(a+t^2 ))) ((√a)/a)[arctg((1/( (√a))))]−∫_0 ^1 (t^2 /((1+t^2 )(a+t^2 )))dt (t^2 /((1+t^2 )(a+t^2 )))=(α/(1+t^2 ))+(β/(a+t^2 ))=((α(a+t^2 )+β(1+t^2 ))/((1+t^2 )(a+t^2 ))) =((t^2 (α+β)+αa+β)/((1+t^2 )(a+t^2 ))) α+β=1 et αa+β=0 α−αa=1→α(1−a)=1→α=−(1/(a−1)) β=(a/(a−1)) f′(a)=∫_0 ^1 (1/(a+t^2 ))−[−(1/(a−1))∫_0 ^1 (1/(1+t^2 ))+(a/(a−1))∫_0 ^1 (1/(a+t^2 ))dt] =(1+(a/(a−1)))∫_0 ^1 (1/(a+t^2 ))+(1/(a−1)).(π/4) =(π/(4(a−1)))+((1/a)+(1/(a−1)))∫_0 ^1 (1/(1+(t^2 /a))) ∫_0 ^1 (1/(1+(t^2 /a)))=Σ_(n≥0) ∫_0 ^1 (−1)^n ((t^2 /a))^n =Σ_(n≥0) (((−1)^n )/a^n ) f′(a)=(π/(4(a−1)))+((1/a)+(1/(a−1)))Σ_(n≥0) (((−1)^n )/a^n ) f(a)=(π/4)ln(a−1)+Σ_(n≥1) (−1)^(n+1) (1/(na^n ))+Σ_(n≥0) ∫(((−1)^n )/(a^(n+1) −a^n ))da](https://www.tinkutara.com/question/Q167600.png)
$${f}\left({a}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({a}+{tan}^{\mathrm{2}} {x}\right){dx} \\ $$$${f}'\left({a}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{{a}+{tan}^{\mathrm{2}} {x}}{dx} \\ $$$${t}={tanx}\rightarrow{dt}=\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{a}+{t}^{\mathrm{2}} }.\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{a}+{t}^{\mathrm{2}} }.\left[\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right]{dt} \\ $$$$\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+\left(\frac{{t}}{\:\sqrt{{a}}}\right)^{\mathrm{2}} }{dt}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left({a}+{t}^{\mathrm{2}} \right)} \\ $$$$\frac{\sqrt{{a}}}{{a}}\left[{arctg}\left(\frac{\mathrm{1}}{\:\sqrt{{a}}}\right)\right]−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left({a}+{t}^{\mathrm{2}} \right)}{dt} \\ $$$$\frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left({a}+{t}^{\mathrm{2}} \right)}=\frac{\alpha}{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\beta}{{a}+{t}^{\mathrm{2}} }=\frac{\alpha\left({a}+{t}^{\mathrm{2}} \right)+\beta\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left({a}+{t}^{\mathrm{2}} \right)} \\ $$$$=\frac{{t}^{\mathrm{2}} \left(\alpha+\beta\right)+\alpha{a}+\beta}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left({a}+{t}^{\mathrm{2}} \right)} \\ $$$$\alpha+\beta=\mathrm{1}\:{et}\:\alpha{a}+\beta=\mathrm{0} \\ $$$$\alpha−\alpha{a}=\mathrm{1}\rightarrow\alpha\left(\mathrm{1}−{a}\right)=\mathrm{1}\rightarrow\alpha=−\frac{\mathrm{1}}{{a}−\mathrm{1}} \\ $$$$\beta=\frac{{a}}{{a}−\mathrm{1}} \\ $$$${f}'\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{a}+{t}^{\mathrm{2}} }−\left[−\frac{\mathrm{1}}{{a}−\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{{a}}{{a}−\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{a}+{t}^{\mathrm{2}} }{dt}\right] \\ $$$$\:\:=\left(\mathrm{1}+\frac{{a}}{{a}−\mathrm{1}}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{a}+{t}^{\mathrm{2}} }+\frac{\mathrm{1}}{{a}−\mathrm{1}}.\frac{\pi}{\mathrm{4}} \\ $$$$\:\:=\frac{\pi}{\mathrm{4}\left({a}−\mathrm{1}\right)}+\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{a}−\mathrm{1}}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+\frac{{t}^{\mathrm{2}} }{{a}}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+\frac{{t}^{\mathrm{2}} }{{a}}}=\underset{{n}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{{n}} \left(\frac{{t}^{\mathrm{2}} }{{a}}\right)^{{n}} =\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{{a}^{{n}} } \\ $$$${f}'\left({a}\right)=\frac{\pi}{\mathrm{4}\left({a}−\mathrm{1}\right)}+\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{a}−\mathrm{1}}\right)\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{{a}^{{n}} } \\ $$$${f}\left({a}\right)=\frac{\pi}{\mathrm{4}}{ln}\left({a}−\mathrm{1}\right)+\underset{{n}\geqslant\mathrm{1}} {\sum}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\mathrm{1}}{{na}^{{n}} }+\underset{{n}\geqslant\mathrm{0}} {\sum}\int\frac{\left(−\mathrm{1}\right)^{{n}} }{{a}^{{n}+\mathrm{1}} −{a}^{{n}} }{da} \\ $$$$ \\ $$
