Menu Close

Express-2-sin-cos-6-in-the-form-sin-A-sin-B-i-using-that-result-prove-that-2sin-cos-6-cos-4-cos-2-sin-7-sin-ii-deduce-the-result-cos-12pi-7-cos-8pi-7-cos-4pi

Tinku Tara 0 Comments
Pin




Question Number 101040 by Rio Michael last updated on 30/Jun/20
Express 2 sin θ cos 6θ in the form sin A − sin B (i) using that result prove that 2sin θ( cos 6θ + cos 4θ + cos 2θ) = sin 7θ−sin θ (ii) deduce the result cos (((12π)/7)) + cos (((8π)/7)) + cos (((4π)/7)) = −(1/2) (iii) hence find a general solution to ((sin7θ − sin θ)/(cos 6θ + cos 4θ + cos 2θ)) = 1
$$\:\mathrm{Express}\:\mathrm{2}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\mathrm{6}\theta\:\mathrm{in}\:\mathrm{the}\:\mathrm{form}\:\:\mathrm{sin}\:{A}\:−\:\mathrm{sin}\:{B} \\ $$$$\left({i}\right)\:\mathrm{using}\:\mathrm{that}\:\mathrm{result}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{2sin}\:\theta\left(\:\mathrm{cos}\:\mathrm{6}\theta\:+\:\mathrm{cos}\:\mathrm{4}\theta\:+\:\mathrm{cos}\:\mathrm{2}\theta\right)\:=\:\mathrm{sin}\:\mathrm{7}\theta−\mathrm{sin}\:\theta \\ $$$$\left({ii}\right)\:\mathrm{deduce}\:\mathrm{the}\:\mathrm{result}\:\mathrm{cos}\:\left(\frac{\mathrm{12}\pi}{\mathrm{7}}\right)\:+\:\mathrm{cos}\:\left(\frac{\mathrm{8}\pi}{\mathrm{7}}\right)\:+\:\mathrm{cos}\:\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right)\:=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left({iii}\right)\:\mathrm{hence}\:\mathrm{find}\:\mathrm{a}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{to}\:\frac{\mathrm{sin7}\theta\:−\:\mathrm{sin}\:\theta}{\mathrm{cos}\:\mathrm{6}\theta\:+\:\mathrm{cos}\:\mathrm{4}\theta\:+\:\mathrm{cos}\:\mathrm{2}\theta}\:=\:\mathrm{1} \\ $$
Answered by maths mind last updated on 30/Jun/20
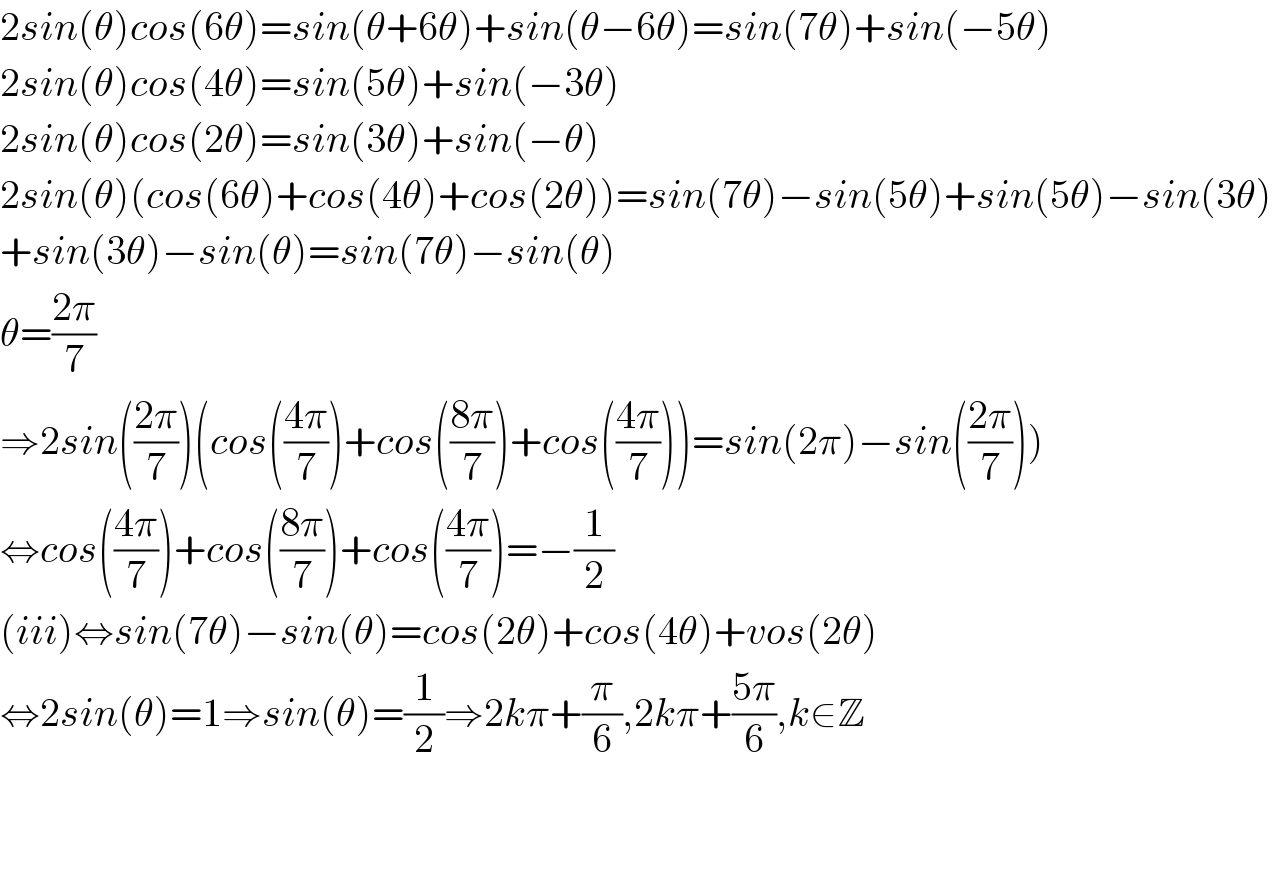
2sin(θ)cos(6θ)=sin(θ+6θ)+sin(θ−6θ)=sin(7θ)+sin(−5θ) 2sin(θ)cos(4θ)=sin(5θ)+sin(−3θ) 2sin(θ)cos(2θ)=sin(3θ)+sin(−θ) 2sin(θ)(cos(6θ)+cos(4θ)+cos(2θ))=sin(7θ)−sin(5θ)+sin(5θ)−sin(3θ) +sin(3θ)−sin(θ)=sin(7θ)−sin(θ) θ=((2π)/7) ⇒2sin(((2π)/7))(cos(((4π)/7))+cos(((8π)/7))+cos(((4π)/7)))=sin(2π)−sin(((2π)/7))) ⇔cos(((4π)/7))+cos(((8π)/7))+cos(((4π)/7))=−(1/2) (iii)⇔sin(7θ)−sin(θ)=cos(2θ)+cos(4θ)+vos(2θ) ⇔2sin(θ)=1⇒sin(θ)=(1/2)⇒2kπ+(π/6),2kπ+((5π)/6),k∈Z
$$\mathrm{2}{sin}\left(\theta\right){cos}\left(\mathrm{6}\theta\right)={sin}\left(\theta+\mathrm{6}\theta\right)+{sin}\left(\theta−\mathrm{6}\theta\right)={sin}\left(\mathrm{7}\theta\right)+{sin}\left(−\mathrm{5}\theta\right) \\ $$$$\mathrm{2}{sin}\left(\theta\right){cos}\left(\mathrm{4}\theta\right)={sin}\left(\mathrm{5}\theta\right)+{sin}\left(−\mathrm{3}\theta\right) \\ $$$$\mathrm{2}{sin}\left(\theta\right){cos}\left(\mathrm{2}\theta\right)={sin}\left(\mathrm{3}\theta\right)+{sin}\left(−\theta\right) \\ $$$$\mathrm{2}{sin}\left(\theta\right)\left({cos}\left(\mathrm{6}\theta\right)+{cos}\left(\mathrm{4}\theta\right)+{cos}\left(\mathrm{2}\theta\right)\right)={sin}\left(\mathrm{7}\theta\right)−{sin}\left(\mathrm{5}\theta\right)+{sin}\left(\mathrm{5}\theta\right)−{sin}\left(\mathrm{3}\theta\right) \\ $$$$+{sin}\left(\mathrm{3}\theta\right)−{sin}\left(\theta\right)={sin}\left(\mathrm{7}\theta\right)−{sin}\left(\theta\right) \\ $$$$\theta=\frac{\mathrm{2}\pi}{\mathrm{7}} \\ $$$$\left.\Rightarrow\mathrm{2}{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)\left({cos}\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right)+{cos}\left(\frac{\mathrm{8}\pi}{\mathrm{7}}\right)+{cos}\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right)\right)={sin}\left(\mathrm{2}\pi\right)−{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)\right) \\ $$$$\Leftrightarrow{cos}\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right)+{cos}\left(\frac{\mathrm{8}\pi}{\mathrm{7}}\right)+{cos}\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right)=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left({iii}\right)\Leftrightarrow{sin}\left(\mathrm{7}\theta\right)−{sin}\left(\theta\right)={cos}\left(\mathrm{2}\theta\right)+{cos}\left(\mathrm{4}\theta\right)+{vos}\left(\mathrm{2}\theta\right) \\ $$$$\Leftrightarrow\mathrm{2}{sin}\left(\theta\right)=\mathrm{1}\Rightarrow{sin}\left(\theta\right)=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{6}},\mathrm{2}{k}\pi+\frac{\mathrm{5}\pi}{\mathrm{6}},{k}\in\mathbb{Z} \\ $$$$ \\ $$$$ \\ $$
Commented by Rio Michael last updated on 30/Jun/20
explicit sir thanks
$$\mathrm{explicit}\:\mathrm{sir}\:\mathrm{thanks} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *