Menu Close

express-2x-2-x-2-x-2-2-1-2x-as-partial-fraction-

Tinku Tara 0 Comments
Pin




Question Number 14421 by chux last updated on 31/May/17
express ((2x^2 −x+2)/((x+2)^2 (1−2x)))as partial fraction
$$\mathrm{express}\:\frac{\mathrm{2x}^{\mathrm{2}} −\mathrm{x}+\mathrm{2}}{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{2x}\right)}\mathrm{as}\:\mathrm{partial} \\ $$$$\mathrm{fraction} \\ $$
Answered by RasheedSindhi last updated on 01/Jun/17
Let ((2x^2 −x+2)/((x+2)^2 (1−2x)))=(A_1 /(x+2))+(A_2 /((x+2)^2 ))+(B/(1−2x)) 2x^2 −x+2=A_1 (x+2)(1−2x)+A_2 (1−2x)+B(x+2)^2 This is an identity i-e it′s equal for all values of x. Let x=−2 2(−2)^2 −(−2)+2=A_2 (1−2(−2)) A_2 =((12)/5) Let x=1/2 2(1/2)^2 −(1/2)+2=B((1/2)+2)^2 B(((25)/4))=(1/2)−(1/2)+2 B=2((4/(25)))=(8/(25)) To determine A_1 : 2x^2 −x+2=A_1 (x+2)(1−2x)+A_2 (1−2x)+B(x+2)^2 Substitute A_2 =((12)/5) & B=(8/(25)) in above. 2x^2 −x+2=A_1 (x+2)(1−2x)+(((12)/5))(1−2x)+((8/(25)))(x+2)^2 25x^2 −25x+50=25A_1 (−2x^2 −3x+2) +60(1+2x)+8(x^2 +4x+4) 25x^2 −25x+50=−50A_1 x^2 −75A_1 x+50A_1 +60+120x+8x^2 +32x+32 25x^2 −25x+50=(−50A_1 +8)x^2 −75A_1 x+50A_1 +60+120x+32x+32 ⊂⊕∩⊤!∩∪∈...
$$\mathrm{Let} \\ $$$$\frac{\mathrm{2x}^{\mathrm{2}} −\mathrm{x}+\mathrm{2}}{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{2x}\right)}=\frac{\mathrm{A}_{\mathrm{1}} }{\mathrm{x}+\mathrm{2}}+\frac{\mathrm{A}_{\mathrm{2}} }{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{B}}{\mathrm{1}−\mathrm{2x}} \\ $$$$\mathrm{2x}^{\mathrm{2}} −\mathrm{x}+\mathrm{2}=\mathrm{A}_{\mathrm{1}} \left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{1}−\mathrm{2x}\right)+\mathrm{A}_{\mathrm{2}} \left(\mathrm{1}−\mathrm{2x}\right)+\mathrm{B}\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{an}\:\mathrm{identity}\:\mathrm{i}-\mathrm{e}\:\mathrm{it}'\mathrm{s}\:\mathrm{equal} \\ $$$$\mathrm{for}\:\mathrm{all}\:\mathrm{values}\:\mathrm{of}\:\mathrm{x}. \\ $$$$\mathrm{Let}\:\mathrm{x}=−\mathrm{2} \\ $$$$\mathrm{2}\left(−\mathrm{2}\right)^{\mathrm{2}} −\left(−\mathrm{2}\right)+\mathrm{2}=\mathrm{A}_{\mathrm{2}} \left(\mathrm{1}−\mathrm{2}\left(−\mathrm{2}\right)\right) \\ $$$$\mathrm{A}_{\mathrm{2}} =\frac{\mathrm{12}}{\mathrm{5}} \\ $$$$\mathrm{Let}\:\mathrm{x}=\mathrm{1}/\mathrm{2} \\ $$$$\mathrm{2}\left(\mathrm{1}/\mathrm{2}\right)^{\mathrm{2}} −\left(\mathrm{1}/\mathrm{2}\right)+\mathrm{2}=\mathrm{B}\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\mathrm{B}\left(\frac{\mathrm{25}}{\mathrm{4}}\right)=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2} \\ $$$$\mathrm{B}=\mathrm{2}\left(\frac{\mathrm{4}}{\mathrm{25}}\right)=\frac{\mathrm{8}}{\mathrm{25}} \\ $$$$\mathrm{To}\:\mathrm{determine}\:\mathrm{A}_{\mathrm{1}} : \\ $$$$\mathrm{2x}^{\mathrm{2}} −\mathrm{x}+\mathrm{2}=\mathrm{A}_{\mathrm{1}} \left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{1}−\mathrm{2x}\right)+\mathrm{A}_{\mathrm{2}} \left(\mathrm{1}−\mathrm{2x}\right)+\mathrm{B}\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\mathrm{Substitute}\:\mathrm{A}_{\mathrm{2}} =\frac{\mathrm{12}}{\mathrm{5}}\:\&\:\mathrm{B}=\frac{\mathrm{8}}{\mathrm{25}}\:\mathrm{in}\:\mathrm{above}. \\ $$$$\mathrm{2x}^{\mathrm{2}} −\mathrm{x}+\mathrm{2}=\mathrm{A}_{\mathrm{1}} \left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{1}−\mathrm{2x}\right)+\left(\frac{\mathrm{12}}{\mathrm{5}}\right)\left(\mathrm{1}−\mathrm{2x}\right)+\left(\frac{\mathrm{8}}{\mathrm{25}}\right)\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\mathrm{25x}^{\mathrm{2}} −\mathrm{25x}+\mathrm{50}=\mathrm{25A}_{\mathrm{1}} \left(−\mathrm{2x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{60}\left(\mathrm{1}+\mathrm{2x}\right)+\mathrm{8}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{4}\right) \\ $$$$\mathrm{25x}^{\mathrm{2}} −\mathrm{25x}+\mathrm{50}=−\mathrm{50A}_{\mathrm{1}} \mathrm{x}^{\mathrm{2}} −\mathrm{75A}_{\mathrm{1}} \mathrm{x}+\mathrm{50A}_{\mathrm{1}} +\mathrm{60}+\mathrm{120x}+\mathrm{8x}^{\mathrm{2}} +\mathrm{32x}+\mathrm{32} \\ $$$$\mathrm{25x}^{\mathrm{2}} −\mathrm{25x}+\mathrm{50}=\left(−\mathrm{50A}_{\mathrm{1}} +\mathrm{8}\right)\mathrm{x}^{\mathrm{2}} −\mathrm{75A}_{\mathrm{1}} \mathrm{x}+\mathrm{50A}_{\mathrm{1}} +\mathrm{60}+\mathrm{120x}+\mathrm{32x}+\mathrm{32} \\ $$$$ \\ $$$$ \\ $$$$\subset\oplus\cap\top!\cap\cup\in… \\ $$
Commented by Tinkutara last updated on 31/May/17
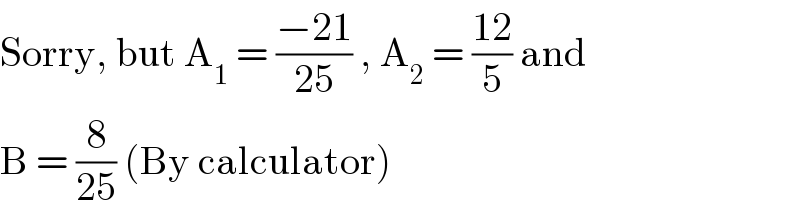
Sorry, but A_1 = ((−21)/(25)) , A_2 = ((12)/5) and B = (8/(25)) (By calculator)
$$\mathrm{Sorry},\:\mathrm{but}\:\mathrm{A}_{\mathrm{1}} \:=\:\frac{−\mathrm{21}}{\mathrm{25}}\:,\:\mathrm{A}_{\mathrm{2}} \:=\:\frac{\mathrm{12}}{\mathrm{5}}\:\mathrm{and} \\ $$$$\mathrm{B}\:=\:\frac{\mathrm{8}}{\mathrm{25}}\:\left(\mathrm{By}\:\mathrm{calculator}\right) \\ $$
Commented by chux last updated on 01/Jun/17
thank you very much sir
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *