Menu Close

express-7x-4-x-3-x-2-9x-9-in-partial-fraction-

Tinku Tara 0 Comments
Pin




Question Number 35245 by JOHNMASANJA last updated on 17/May/18
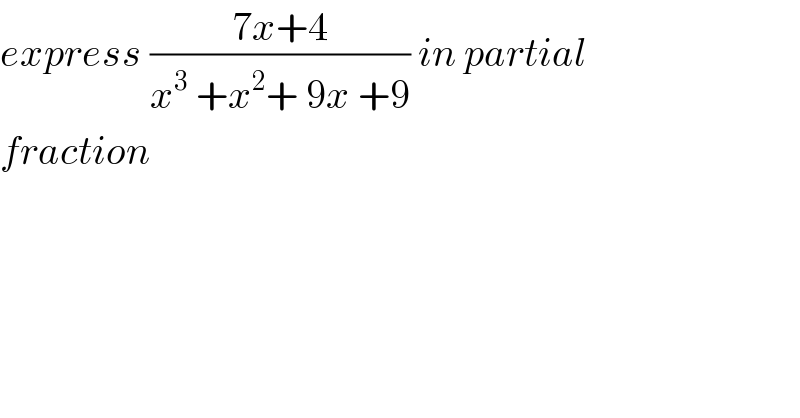
express ((7x+4)/(x^3 +x^2 + 9x +9)) in partial fraction
$${express}\:\frac{\mathrm{7}{x}+\mathrm{4}}{{x}^{\mathrm{3}} \:+{x}^{\mathrm{2}} +\:\mathrm{9}{x}\:+\mathrm{9}}\:{in}\:{partial} \\ $$$${fraction} \\ $$
Commented by Rasheed.Sindhi last updated on 17/May/18
prof Abdo imad Use of limit in partial fractions is new for me.Could you please insert more steps to discribe 4th,5th & 6th lines?
$$\mathrm{prof}\:\mathrm{Abdo}\:\mathrm{imad} \\ $$$$\mathrm{Use}\:\mathrm{of}\:\mathrm{limit}\:\mathrm{in}\:\mathrm{partial}\:\mathrm{fractions}\:\mathrm{is}\:\mathrm{new} \\ $$$$\mathrm{for}\:\mathrm{me}.\mathrm{Could}\:\mathrm{you}\:\mathrm{please}\:\mathrm{insert}\:\mathrm{more} \\ $$$$\mathrm{steps}\:\mathrm{to}\:\mathrm{discribe}\:\mathrm{4th},\mathrm{5th}\:\&\:\mathrm{6th}\:\mathrm{lines}? \\ $$
Commented by Rasheed.Sindhi last updated on 17/May/18
Sir th∝nk$ a ⌊♥⊤! BTW prof Abdo imad=^(?) abdo mathsup 649 cc =^(?) math khazana by abdo =^(?) abdo.msup.com =^(?) ID containing ′abdo′ ???
$$\mathrm{Sir}\:\mathrm{th}\propto\mathrm{n}\Bbbk\$\:\mathrm{a}\:\lfloor\heartsuit\top!\: \\ $$$$\mathrm{BTW}\: \\ $$$$\mathrm{prof}\:\mathrm{Abdo}\:\mathrm{imad}\overset{?} {=}\mathrm{abdo}\:\mathrm{mathsup}\:\mathrm{649}\:\mathrm{cc} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\overset{?} {=}\mathrm{math}\:\mathrm{khazana}\:\mathrm{by}\:\mathrm{abdo} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\overset{?} {=}\mathrm{abdo}.\mathrm{msup}.\mathrm{com} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\overset{?} {=}\mathrm{ID}\:\mathrm{containing}\:'\mathrm{abdo}' \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:??? \\ $$
Commented by prof Abdo imad last updated on 17/May/18
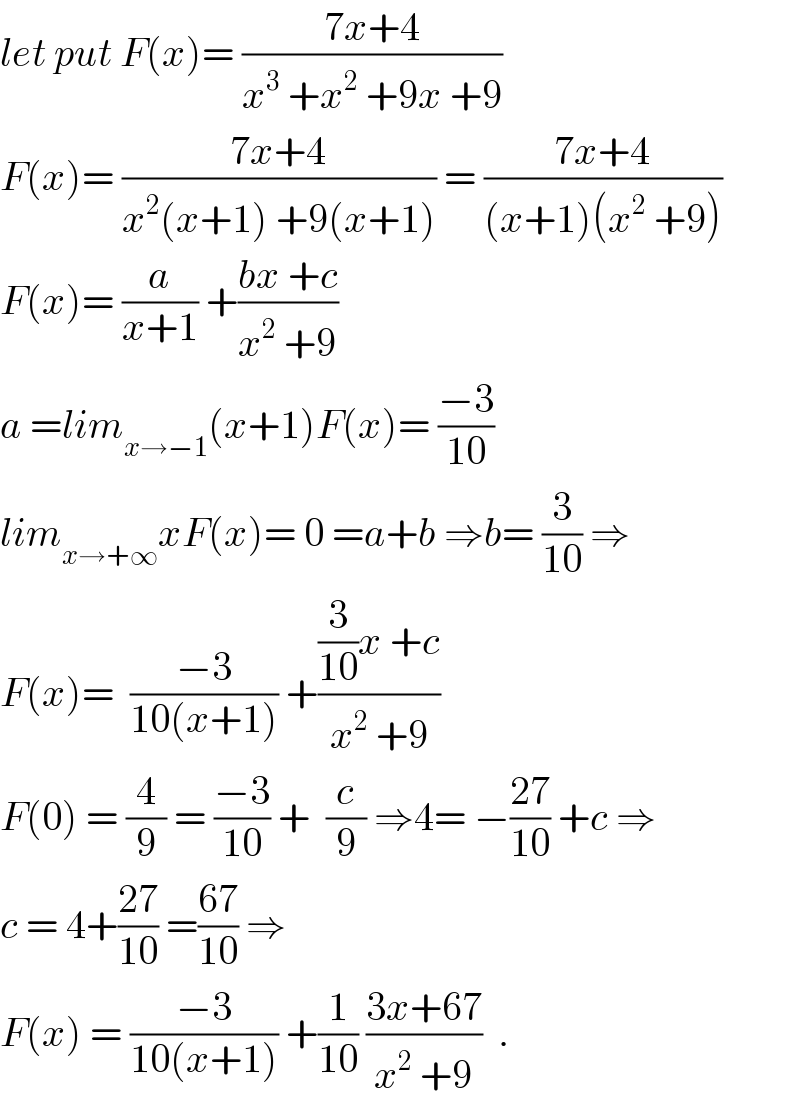
let put F(x)= ((7x+4)/(x^3 +x^2 +9x +9)) F(x)= ((7x+4)/(x^2 (x+1) +9(x+1))) = ((7x+4)/((x+1)(x^2 +9))) F(x)= (a/(x+1)) +((bx +c)/(x^2 +9)) a =lim_(x→−1) (x+1)F(x)= ((−3)/(10)) lim_(x→+∞) xF(x)= 0 =a+b ⇒b= (3/(10)) ⇒ F(x)= ((−3)/(10(x+1))) +(((3/(10))x +c)/(x^2 +9)) F(0) = (4/9) = ((−3)/(10)) + (c/9) ⇒4= −((27)/(10)) +c ⇒ c = 4+((27)/(10)) =((67)/(10)) ⇒ F(x) = ((−3)/(10(x+1))) +(1/(10)) ((3x+67)/(x^2 +9)) .
$${let}\:{put}\:{F}\left({x}\right)=\:\frac{\mathrm{7}{x}+\mathrm{4}}{{x}^{\mathrm{3}} \:+{x}^{\mathrm{2}} \:+\mathrm{9}{x}\:+\mathrm{9}} \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{7}{x}+\mathrm{4}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)\:+\mathrm{9}\left({x}+\mathrm{1}\right)}\:=\:\frac{\mathrm{7}{x}+\mathrm{4}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\mathrm{9}\right)} \\ $$$${F}\left({x}\right)=\:\frac{{a}}{{x}+\mathrm{1}}\:+\frac{{bx}\:+{c}}{{x}^{\mathrm{2}} \:+\mathrm{9}} \\ $$$${a}\:={lim}_{{x}\rightarrow−\mathrm{1}} \left({x}+\mathrm{1}\right){F}\left({x}\right)=\:\frac{−\mathrm{3}}{\mathrm{10}} \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)=\:\mathrm{0}\:={a}+{b}\:\Rightarrow{b}=\:\frac{\mathrm{3}}{\mathrm{10}}\:\Rightarrow \\ $$$${F}\left({x}\right)=\:\:\frac{−\mathrm{3}}{\mathrm{10}\left({x}+\mathrm{1}\right)}\:+\frac{\frac{\mathrm{3}}{\mathrm{10}}{x}\:+{c}}{{x}^{\mathrm{2}} \:+\mathrm{9}} \\ $$$${F}\left(\mathrm{0}\right)\:=\:\frac{\mathrm{4}}{\mathrm{9}}\:=\:\frac{−\mathrm{3}}{\mathrm{10}}\:+\:\:\frac{{c}}{\mathrm{9}}\:\Rightarrow\mathrm{4}=\:−\frac{\mathrm{27}}{\mathrm{10}}\:+{c}\:\Rightarrow \\ $$$${c}\:=\:\mathrm{4}+\frac{\mathrm{27}}{\mathrm{10}}\:=\frac{\mathrm{67}}{\mathrm{10}}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\:\frac{−\mathrm{3}}{\mathrm{10}\left({x}+\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{10}}\:\frac{\mathrm{3}{x}+\mathrm{67}}{{x}^{\mathrm{2}} \:+\mathrm{9}}\:\:. \\ $$
Commented by Rasheed.Sindhi last updated on 17/May/18
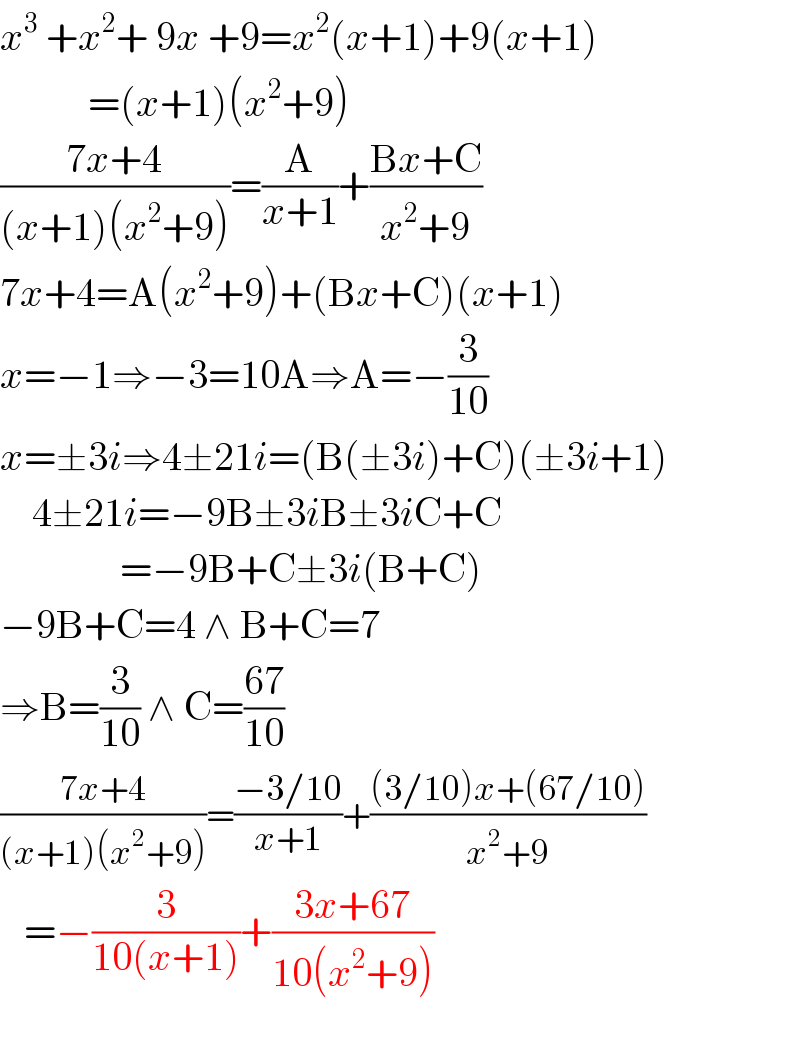
x^3 +x^2 + 9x +9=x^2 (x+1)+9(x+1) =(x+1)(x^2 +9) ((7x+4)/((x+1)(x^2 +9)))=(A/(x+1))+((Bx+C)/(x^2 +9)) 7x+4=A(x^2 +9)+(Bx+C)(x+1) x=−1⇒−3=10A⇒A=−(3/(10)) x=±3i⇒4±21i=(B(±3i)+C)(±3i+1) 4±21i=−9B±3iB±3iC+C =−9B+C±3i(B+C) −9B+C=4 ∧ B+C=7 ⇒B=(3/(10)) ∧ C=((67)/(10)) ((7x+4)/((x+1)(x^2 +9)))=((−3/10)/(x+1))+(((3/10)x+(67/10))/(x^2 +9)) =−(3/(10(x+1)))+((3x+67)/(10(x^2 +9)))
$${x}^{\mathrm{3}} \:+{x}^{\mathrm{2}} +\:\mathrm{9}{x}\:+\mathrm{9}={x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)+\mathrm{9}\left({x}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{9}\right) \\ $$$$\frac{\mathrm{7}{x}+\mathrm{4}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{9}\right)}=\frac{\mathrm{A}}{{x}+\mathrm{1}}+\frac{\mathrm{B}{x}+\mathrm{C}}{{x}^{\mathrm{2}} +\mathrm{9}} \\ $$$$\mathrm{7}{x}+\mathrm{4}=\mathrm{A}\left({x}^{\mathrm{2}} +\mathrm{9}\right)+\left(\mathrm{B}{x}+\mathrm{C}\right)\left({x}+\mathrm{1}\right) \\ $$$${x}=−\mathrm{1}\Rightarrow−\mathrm{3}=\mathrm{10A}\Rightarrow\mathrm{A}=−\frac{\mathrm{3}}{\mathrm{10}} \\ $$$${x}=\pm\mathrm{3}{i}\Rightarrow\mathrm{4}\pm\mathrm{21}{i}=\left(\mathrm{B}\left(\pm\mathrm{3}{i}\right)+\mathrm{C}\right)\left(\pm\mathrm{3}{i}+\mathrm{1}\right) \\ $$$$\:\:\:\:\mathrm{4}\pm\mathrm{21}{i}=−\mathrm{9B}\pm\mathrm{3}{i}\mathrm{B}\pm\mathrm{3}{i}\mathrm{C}+\mathrm{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\mathrm{9B}+\mathrm{C}\pm\mathrm{3}{i}\left(\mathrm{B}+\mathrm{C}\right) \\ $$$$−\mathrm{9B}+\mathrm{C}=\mathrm{4}\:\wedge\:\mathrm{B}+\mathrm{C}=\mathrm{7} \\ $$$$\Rightarrow\mathrm{B}=\frac{\mathrm{3}}{\mathrm{10}}\:\wedge\:\mathrm{C}=\frac{\mathrm{67}}{\mathrm{10}} \\ $$$$\frac{\mathrm{7}{x}+\mathrm{4}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{9}\right)}=\frac{−\mathrm{3}/\mathrm{10}}{{x}+\mathrm{1}}+\frac{\left(\mathrm{3}/\mathrm{10}\right){x}+\left(\mathrm{67}/\mathrm{10}\right)}{{x}^{\mathrm{2}} +\mathrm{9}} \\ $$$$\:\:\:=−\frac{\mathrm{3}}{\mathrm{10}\left({x}+\mathrm{1}\right)}+\frac{\mathrm{3}{x}+\mathrm{67}}{\mathrm{10}\left({x}^{\mathrm{2}} +\mathrm{9}\right)} \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 18/May/18
⊤∦∀∩∣⟨$!
$$\top\nparallel\forall\cap\mid\langle\$! \\ $$
Commented by abdo mathsup 649 cc last updated on 17/May/18
sir Resheed this method is general and easy for a we have F(x)= (a/(x+1)) +((bx+c)/(x^2 +9)) ⇒ lim_(x→−1) (x+1)F(x) = a +lim_(x→−1) (x+1)((bx+c)/(x^2 +9)) =a from another side lim_(x→−1) (x+1)F(x)=lim_(x→−1) ((7x+4)/(x^2 +9)) =((−3)/(10)).... we do the same for b and c...
$${sir}\:{Resheed}\:\:{this}\:{method}\:{is}\:{general}\:{and}\:{easy}\: \\ $$$${for}\:{a}\:\:{we}\:{have}\:\:{F}\left({x}\right)=\:\frac{{a}}{{x}+\mathrm{1}}\:+\frac{{bx}+{c}}{{x}^{\mathrm{2}} \:+\mathrm{9}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow−\mathrm{1}} \left({x}+\mathrm{1}\right){F}\left({x}\right)\:=\:{a}\:+{lim}_{{x}\rightarrow−\mathrm{1}} \left({x}+\mathrm{1}\right)\frac{{bx}+{c}}{{x}^{\mathrm{2}} \:+\mathrm{9}} \\ $$$$={a}\:{from}\:{another}\:{side}\: \\ $$$${lim}_{{x}\rightarrow−\mathrm{1}} \left({x}+\mathrm{1}\right){F}\left({x}\right)={lim}_{{x}\rightarrow−\mathrm{1}} \:\:\:\:\frac{\mathrm{7}{x}+\mathrm{4}}{{x}^{\mathrm{2}} \:+\mathrm{9}}\:=\frac{−\mathrm{3}}{\mathrm{10}}…. \\ $$$${we}\:{do}\:{the}\:{same}\:{for}\:\:{b}\:{and}\:{c}… \\ $$
Commented by abdo mathsup 649 cc last updated on 17/May/18
yes yesall this profils are for me but not all ID containing abdo....
$${yes}\:{yesall}\:{this}\:{profils}\:{are}\:{for}\:{me}\:{but}\:{not}\:{all}\:{ID} \\ $$$${containing}\:{abdo}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *