Question Number 60765 by readone97 last updated on 25/May/19
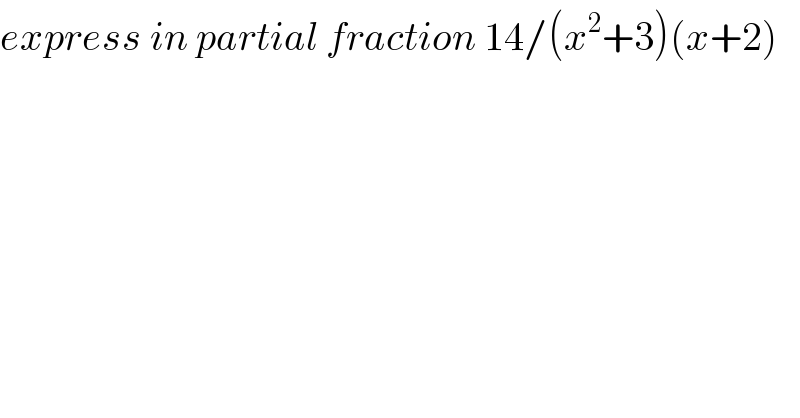
$${express}\:{in}\:{partial}\:{fraction}\:\mathrm{14}/\left({x}^{\mathrm{2}} +\mathrm{3}\right)\left({x}+\mathrm{2}\right) \\ $$
Commented by Prithwish sen last updated on 25/May/19

$$\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3}\right)\left(\mathrm{x}+\mathrm{2}\right)}\:=\:\frac{\mathrm{A}}{\left(\mathrm{x}+\mathrm{2}\right)}\:+\frac{\mathrm{Bx}+\mathrm{C}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3}\right)} \\ $$
Commented by maxmathsup by imad last updated on 25/May/19
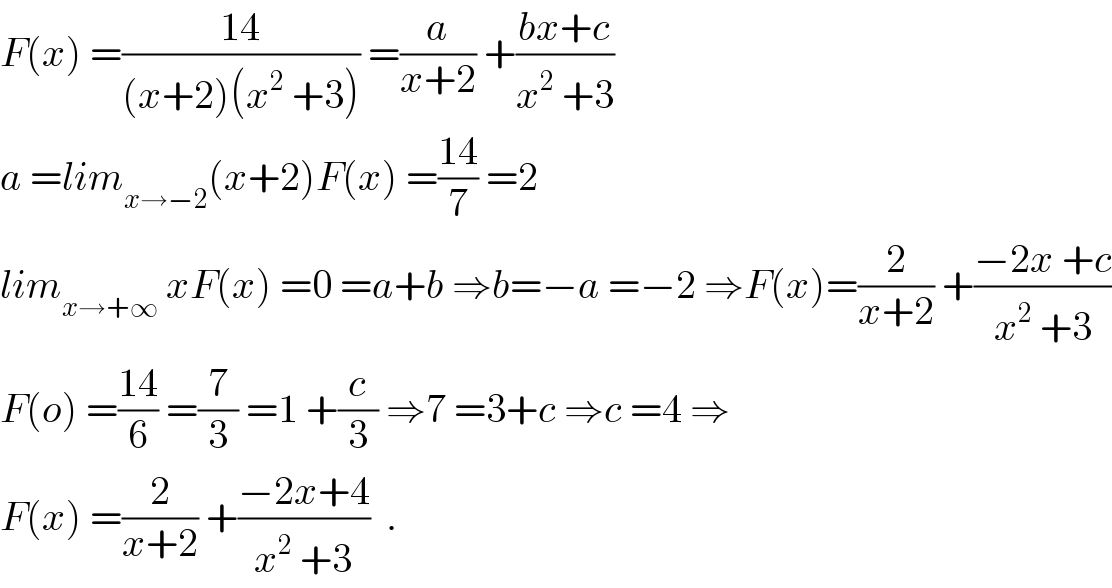
$${F}\left({x}\right)\:=\frac{\mathrm{14}}{\left({x}+\mathrm{2}\right)\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)}\:=\frac{{a}}{{x}+\mathrm{2}}\:+\frac{{bx}+{c}}{{x}^{\mathrm{2}} \:+\mathrm{3}} \\ $$$${a}\:={lim}_{{x}\rightarrow−\mathrm{2}} \left({x}+\mathrm{2}\right){F}\left({x}\right)\:=\frac{\mathrm{14}}{\mathrm{7}}\:=\mathrm{2} \\ $$$${lim}_{{x}\rightarrow+\infty} \:{xF}\left({x}\right)\:=\mathrm{0}\:={a}+{b}\:\Rightarrow{b}=−{a}\:=−\mathrm{2}\:\Rightarrow{F}\left({x}\right)=\frac{\mathrm{2}}{{x}+\mathrm{2}}\:+\frac{−\mathrm{2}{x}\:+{c}}{{x}^{\mathrm{2}} \:+\mathrm{3}} \\ $$$${F}\left({o}\right)\:=\frac{\mathrm{14}}{\mathrm{6}}\:=\frac{\mathrm{7}}{\mathrm{3}}\:=\mathrm{1}\:+\frac{{c}}{\mathrm{3}}\:\Rightarrow\mathrm{7}\:=\mathrm{3}+{c}\:\Rightarrow{c}\:=\mathrm{4}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\frac{\mathrm{2}}{{x}+\mathrm{2}}\:+\frac{−\mathrm{2}{x}+\mathrm{4}}{{x}^{\mathrm{2}} \:+\mathrm{3}}\:\:. \\ $$
