Question Number 180295 by Mastermind last updated on 10/Nov/22

$$\mathrm{Express}\:\mathrm{these}\:\mathrm{both}\:\mathrm{Cartesian}\:\mathrm{and}\: \\ $$$$\mathrm{polar}\:\mathrm{form} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{f}\left(\mathrm{z}\right)=\mathrm{3z}^{\mathrm{2}} −\mathrm{2z}+\frac{\mathrm{1}}{\mathrm{z}} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{f}\left(\mathrm{z}\right)=\mathrm{z}+\frac{\mathrm{1}}{\mathrm{z}} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{Thanks} \\ $$
Commented by Mastermind last updated on 10/Nov/22

$$\mathrm{Express}\:\mathrm{these}\:\mathrm{both}\:\mathrm{in}\:\mathrm{Cartesian}\:\left(\mathrm{z}=\mathrm{x}+\mathrm{iy}\right) \\ $$$$\mathrm{and}\:\mathrm{polar}\:\mathrm{form}\left(\mathrm{z}=\mathrm{re}^{\mathrm{i}\theta} \right) \\ $$$$\left(\mathrm{1}\right)\:\mathrm{f}\left(\mathrm{z}\right)=\mathrm{3z}^{\mathrm{2}} −\mathrm{2z}+\frac{\mathrm{1}}{\mathrm{z}} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{f}\left(\mathrm{z}\right)=\mathrm{z}+\frac{\mathrm{1}}{\mathrm{z}} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{Thanks} \\ $$
Commented by Frix last updated on 10/Nov/22
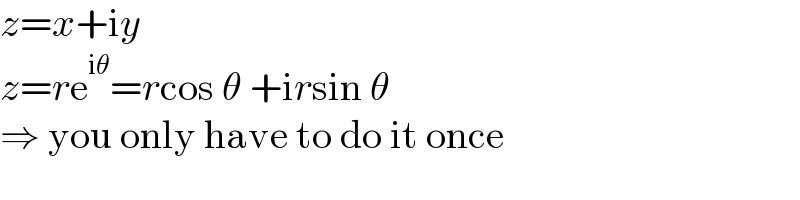
$${z}={x}+\mathrm{i}{y} \\ $$$${z}={r}\mathrm{e}^{\mathrm{i}\theta} ={r}\mathrm{cos}\:\theta\:+\mathrm{i}{r}\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\mathrm{you}\:\mathrm{only}\:\mathrm{have}\:\mathrm{to}\:\mathrm{do}\:\mathrm{it}\:\mathrm{once} \\ $$
