Question Number 56706 by gunawan last updated on 22/Mar/19
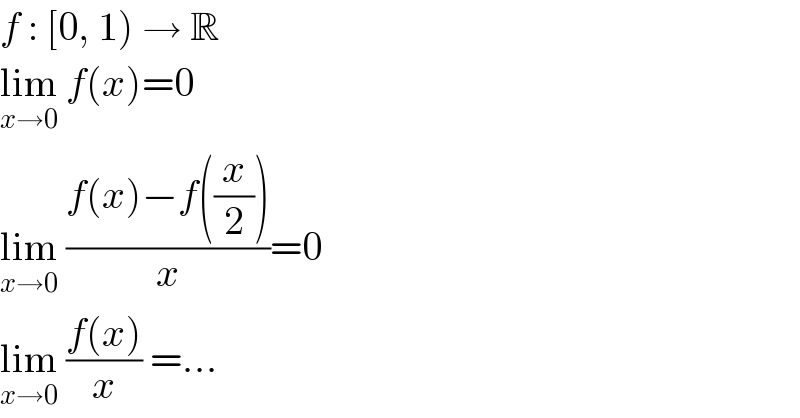
$${f}\::\:\left[\mathrm{0},\:\mathrm{1}\right)\:\rightarrow\:\mathbb{R} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{f}\left({x}\right)=\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{f}\left({x}\right)−{f}\left(\frac{{x}}{\mathrm{2}}\right)}{{x}}=\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{f}\left({x}\right)}{{x}}\:=… \\ $$
Commented by Abdo msup. last updated on 22/Mar/19
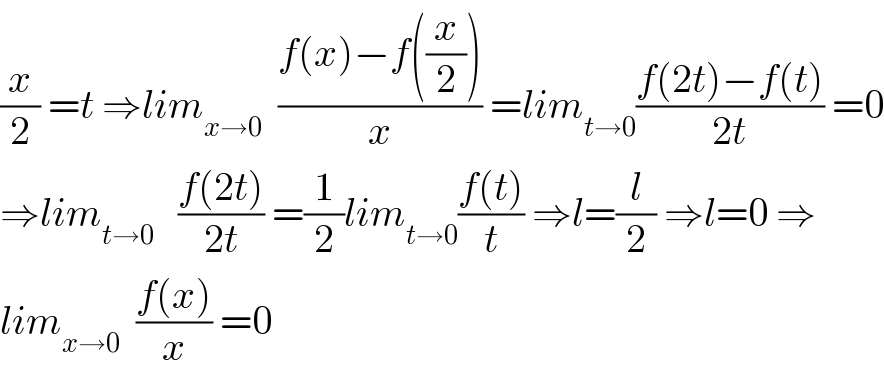
$$\frac{{x}}{\mathrm{2}}\:={t}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{{f}\left({x}\right)−{f}\left(\frac{{x}}{\mathrm{2}}\right)}{{x}}\:={lim}_{{t}\rightarrow\mathrm{0}} \frac{{f}\left(\mathrm{2}{t}\right)−{f}\left({t}\right)}{\mathrm{2}{t}}\:=\mathrm{0} \\ $$$$\Rightarrow{lim}_{{t}\rightarrow\mathrm{0}} \:\:\:\frac{{f}\left(\mathrm{2}{t}\right)}{\mathrm{2}{t}}\:=\frac{\mathrm{1}}{\mathrm{2}}{lim}_{{t}\rightarrow\mathrm{0}} \frac{{f}\left({t}\right)}{{t}}\:\Rightarrow{l}=\frac{{l}}{\mathrm{2}}\:\Rightarrow{l}=\mathrm{0}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{{f}\left({x}\right)}{{x}}\:=\mathrm{0} \\ $$
