Question Number 155281 by mnjuly1970 last updated on 28/Sep/21
![f :[ 0 , 6] → [−4 , 4] f (0 )=0 f (6 )=4 x, y≥0 , x+y ≤6 f (x+y )=(1/4){f(x)(√(16−(f(y))^2 )) +f(y)(√(16−(f(x))^2 )) } ∴ ( f(1) +f (3))^( 2) =?](https://www.tinkutara.com/question/Q155281.png)
$$ \\ $$$$\:{f}\::\left[\:\mathrm{0}\:,\:\:\mathrm{6}\right]\:\rightarrow\:\left[−\mathrm{4}\:,\:\mathrm{4}\right] \\ $$$$\:\:\:{f}\:\left(\mathrm{0}\:\right)=\mathrm{0} \\ $$$$\:\:\:\:{f}\:\left(\mathrm{6}\:\right)=\mathrm{4}\: \\ $$$$\:\:{x},\:\:{y}\geqslant\mathrm{0}\:\:,\:{x}+{y}\:\leqslant\mathrm{6} \\ $$$$\:\:\:{f}\:\left({x}+{y}\:\right)=\frac{\mathrm{1}}{\mathrm{4}}\left\{{f}\left({x}\right)\sqrt{\mathrm{16}−\left({f}\left({y}\right)\right)^{\mathrm{2}} }\:+{f}\left({y}\right)\sqrt{\mathrm{16}−\left({f}\left({x}\right)\right)^{\mathrm{2}} }\:\right\} \\ $$$$\:\:\therefore\:\:\:\left(\:{f}\left(\mathrm{1}\right)\:+{f}\:\left(\mathrm{3}\right)\right)^{\:\mathrm{2}} =? \\ $$
Answered by Rasheed.Sindhi last updated on 29/Sep/21
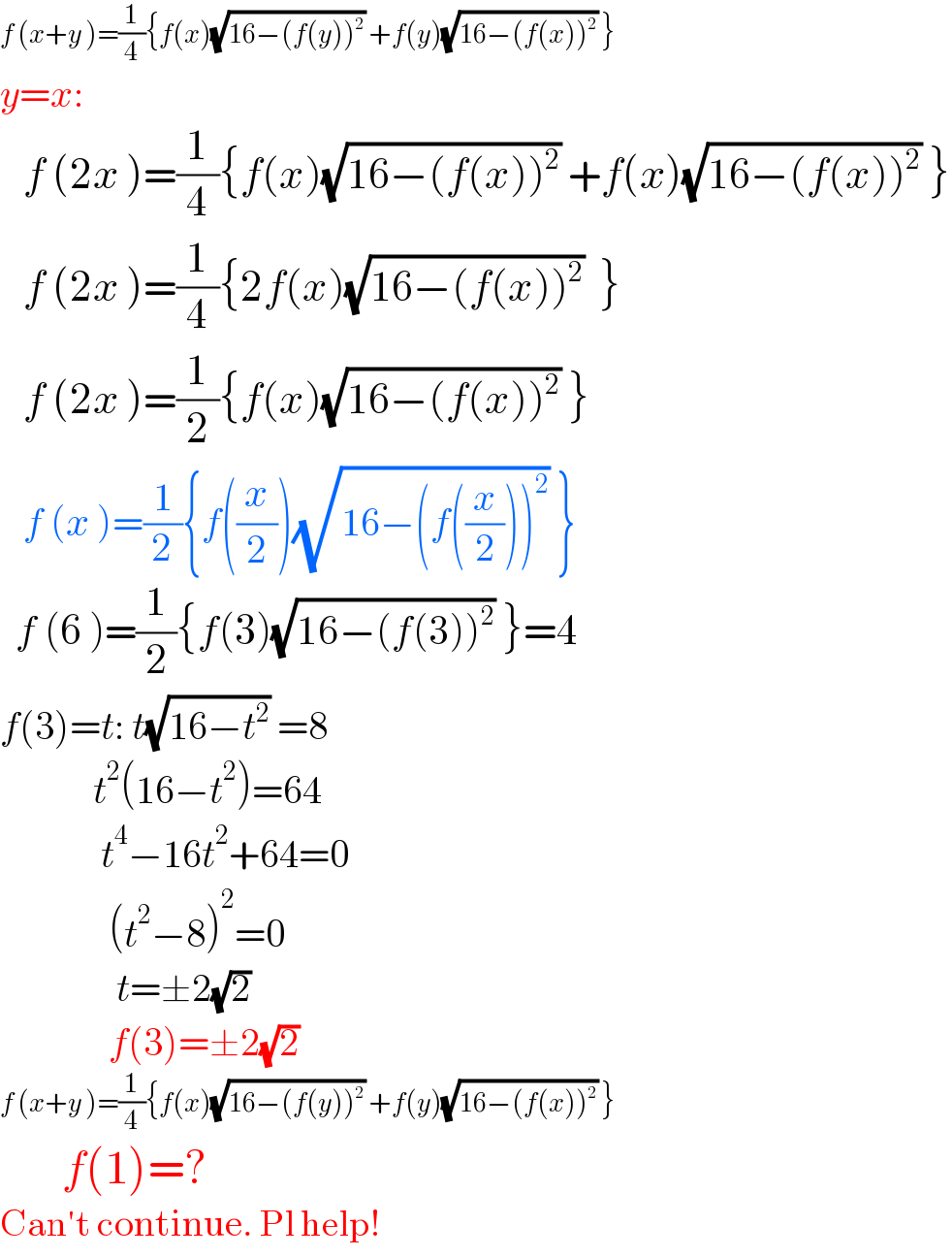
$${f}\:\left({x}+{y}\:\right)=\frac{\mathrm{1}}{\mathrm{4}}\left\{{f}\left({x}\right)\sqrt{\mathrm{16}−\left({f}\left({y}\right)\right)^{\mathrm{2}} }\:+{f}\left({y}\right)\sqrt{\mathrm{16}−\left({f}\left({x}\right)\right)^{\mathrm{2}} }\:\right\} \\ $$$${y}={x}: \\ $$$$\:\:\:{f}\:\left(\mathrm{2}{x}\:\right)=\frac{\mathrm{1}}{\mathrm{4}}\left\{{f}\left({x}\right)\sqrt{\mathrm{16}−\left({f}\left({x}\right)\right)^{\mathrm{2}} }\:+{f}\left({x}\right)\sqrt{\mathrm{16}−\left({f}\left({x}\right)\right)^{\mathrm{2}} }\:\right\} \\ $$$$\:\:\:{f}\:\left(\mathrm{2}{x}\:\right)=\frac{\mathrm{1}}{\mathrm{4}}\left\{\mathrm{2}{f}\left({x}\right)\sqrt{\mathrm{16}−\left({f}\left({x}\right)\right)^{\mathrm{2}} }\:\:\right\} \\ $$$$\:\:\:{f}\:\left(\mathrm{2}{x}\:\right)=\frac{\mathrm{1}}{\mathrm{2}}\left\{{f}\left({x}\right)\sqrt{\mathrm{16}−\left({f}\left({x}\right)\right)^{\mathrm{2}} }\:\right\} \\ $$$$\:\:\:{f}\:\left({x}\:\right)=\frac{\mathrm{1}}{\mathrm{2}}\left\{{f}\left(\frac{{x}}{\mathrm{2}}\right)\sqrt{\mathrm{16}−\left({f}\left(\frac{{x}}{\mathrm{2}}\right)\right)^{\mathrm{2}} }\:\right\} \\ $$$$\:\:{f}\:\left(\mathrm{6}\:\right)=\frac{\mathrm{1}}{\mathrm{2}}\left\{{f}\left(\mathrm{3}\right)\sqrt{\mathrm{16}−\left({f}\left(\mathrm{3}\right)\right)^{\mathrm{2}} }\:\right\}=\mathrm{4} \\ $$$${f}\left(\mathrm{3}\right)={t}:\:{t}\sqrt{\mathrm{16}−{t}^{\mathrm{2}} }\:=\mathrm{8} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{t}^{\mathrm{2}} \left(\mathrm{16}−{t}^{\mathrm{2}} \right)=\mathrm{64} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{t}^{\mathrm{4}} −\mathrm{16}{t}^{\mathrm{2}} +\mathrm{64}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({t}^{\mathrm{2}} −\mathrm{8}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{t}=\pm\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}\left(\mathrm{3}\right)=\pm\mathrm{2}\sqrt{\mathrm{2}} \\ $$$${f}\:\left({x}+{y}\:\right)=\frac{\mathrm{1}}{\mathrm{4}}\left\{{f}\left({x}\right)\sqrt{\mathrm{16}−\left({f}\left({y}\right)\right)^{\mathrm{2}} }\:+{f}\left({y}\right)\sqrt{\mathrm{16}−\left({f}\left({x}\right)\right)^{\mathrm{2}} }\:\right\} \\ $$$$\:\:\:\:\:\:\:\:{f}\left(\mathrm{1}\right)=? \\ $$$$\mathrm{Can}'\mathrm{t}\:\mathrm{continue}.\:\mathrm{Pl}\:\mathrm{help}! \\ $$
