Question Number 147697 by mathdanisur last updated on 22/Jul/21
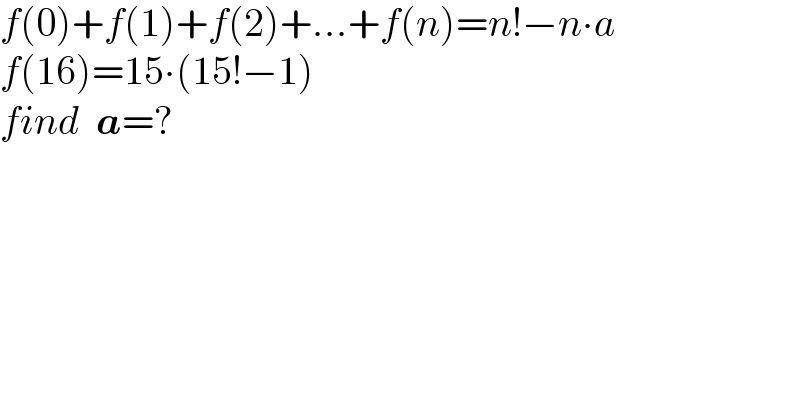
$${f}\left(\mathrm{0}\right)+{f}\left(\mathrm{1}\right)+{f}\left(\mathrm{2}\right)+…+{f}\left({n}\right)={n}!−{n}\centerdot{a} \\ $$$${f}\left(\mathrm{16}\right)=\mathrm{15}\centerdot\left(\mathrm{15}!−\mathrm{1}\right) \\ $$$${find}\:\:\boldsymbol{{a}}=? \\ $$
Answered by Olaf_Thorendsen last updated on 22/Jul/21
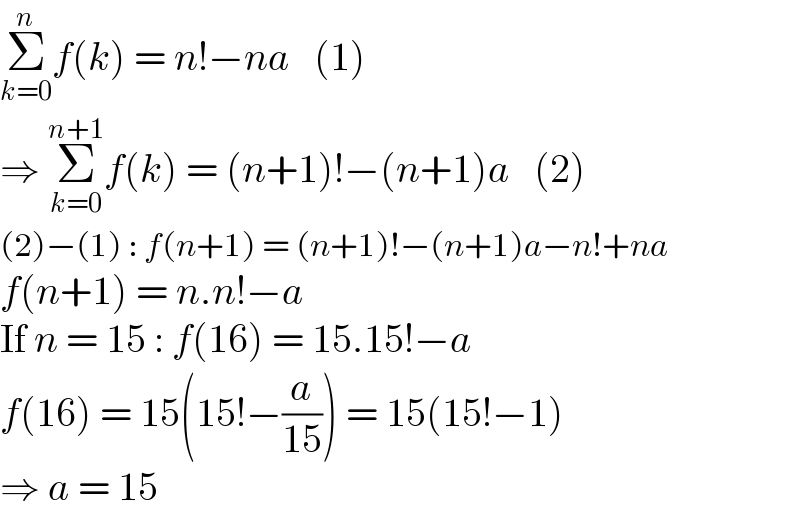
$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{f}\left({k}\right)\:=\:{n}!−{na}\:\:\:\left(\mathrm{1}\right) \\ $$$$\Rightarrow\:\underset{{k}=\mathrm{0}} {\overset{{n}+\mathrm{1}} {\sum}}{f}\left({k}\right)\:=\:\left({n}+\mathrm{1}\right)!−\left({n}+\mathrm{1}\right){a}\:\:\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{2}\right)−\left(\mathrm{1}\right)\::\:{f}\left({n}+\mathrm{1}\right)\:=\:\left({n}+\mathrm{1}\right)!−\left({n}+\mathrm{1}\right){a}−{n}!+{na} \\ $$$${f}\left({n}+\mathrm{1}\right)\:=\:{n}.{n}!−{a} \\ $$$$\mathrm{If}\:{n}\:=\:\mathrm{15}\::\:{f}\left(\mathrm{16}\right)\:=\:\mathrm{15}.\mathrm{15}!−{a} \\ $$$${f}\left(\mathrm{16}\right)\:=\:\mathrm{15}\left(\mathrm{15}!−\frac{{a}}{\mathrm{15}}\right)\:=\:\mathrm{15}\left(\mathrm{15}!−\mathrm{1}\right) \\ $$$$\Rightarrow\:{a}\:=\:\mathrm{15} \\ $$
Commented by mathdanisur last updated on 22/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$
