Question Number 183064 by Matica last updated on 19/Dec/22
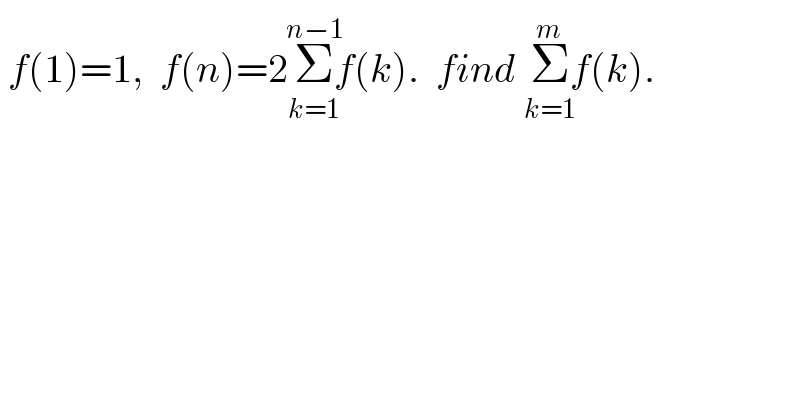
$$\:{f}\left(\mathrm{1}\right)=\mathrm{1},\:\:{f}\left({n}\right)=\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\Sigma}}{f}\left({k}\right).\:\:{find}\:\underset{{k}=\mathrm{1}} {\overset{{m}} {\Sigma}}{f}\left({k}\right). \\ $$
Answered by mr W last updated on 19/Dec/22
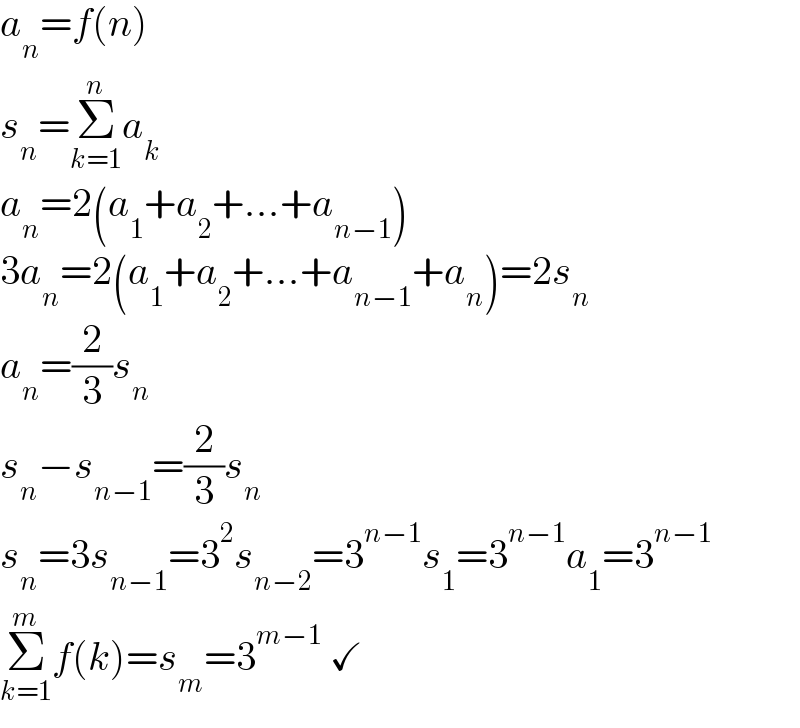
$${a}_{{n}} ={f}\left({n}\right) \\ $$$${s}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k}} \\ $$$${a}_{{n}} =\mathrm{2}\left({a}_{\mathrm{1}} +{a}_{\mathrm{2}} +…+{a}_{{n}−\mathrm{1}} \right) \\ $$$$\mathrm{3}{a}_{{n}} =\mathrm{2}\left({a}_{\mathrm{1}} +{a}_{\mathrm{2}} +…+{a}_{{n}−\mathrm{1}} +{a}_{{n}} \right)=\mathrm{2}{s}_{{n}} \\ $$$${a}_{{n}} =\frac{\mathrm{2}}{\mathrm{3}}{s}_{{n}} \\ $$$${s}_{{n}} −{s}_{{n}−\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{3}}{s}_{{n}} \\ $$$${s}_{{n}} =\mathrm{3}{s}_{{n}−\mathrm{1}} =\mathrm{3}^{\mathrm{2}} {s}_{{n}−\mathrm{2}} =\mathrm{3}^{{n}−\mathrm{1}} {s}_{\mathrm{1}} =\mathrm{3}^{{n}−\mathrm{1}} {a}_{\mathrm{1}} =\mathrm{3}^{{n}−\mathrm{1}} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}{f}\left({k}\right)={s}_{{m}} =\mathrm{3}^{{m}−\mathrm{1}} \:\checkmark \\ $$
Commented by Matica last updated on 19/Dec/22

$${Thank}\:{a}\:{lot}.\: \\ $$
Commented by Matica last updated on 19/Dec/22
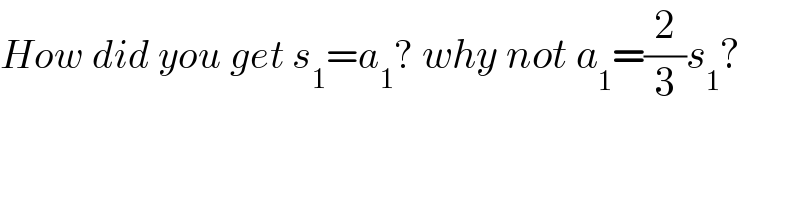
$${How}\:{did}\:{you}\:{get}\:{s}_{\mathrm{1}} ={a}_{\mathrm{1}} ?\:{why}\:{not}\:{a}_{\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{3}}{s}_{\mathrm{1}} ? \\ $$
Commented by mr W last updated on 19/Dec/22

$${s}_{{n}} \:{means}\:{the}\:{sum}\:{of}\:{first}\:{n}\:{terms}. \\ $$$${a}_{\mathrm{1}} =\mathrm{1},\:{s}_{\mathrm{1}} ={a}_{\mathrm{1}} =\mathrm{1} \\ $$$${these}\:{are}\:{given}\:{initial}\:{conditions}. \\ $$$${s}_{\mathrm{1}} \:{is}\:{the}\:{sum}\:{of}\:{the}\:{first}\:{term},\:{it}\:{must} \\ $$$${be}\:{a}_{\mathrm{1}} !\:{or}\:{do}\:{you}\:{think}\:{a}_{\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{3}}{s}_{\mathrm{1}} \:{makes} \\ $$$${any}\:{sense}? \\ $$
Commented by Matica last updated on 19/Dec/22
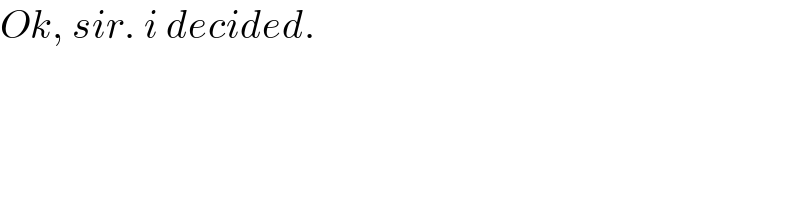
$${Ok},\:{sir}.\:{i}\:{decided}. \\ $$
