Question Number 91578 by jagoll last updated on 01/May/20
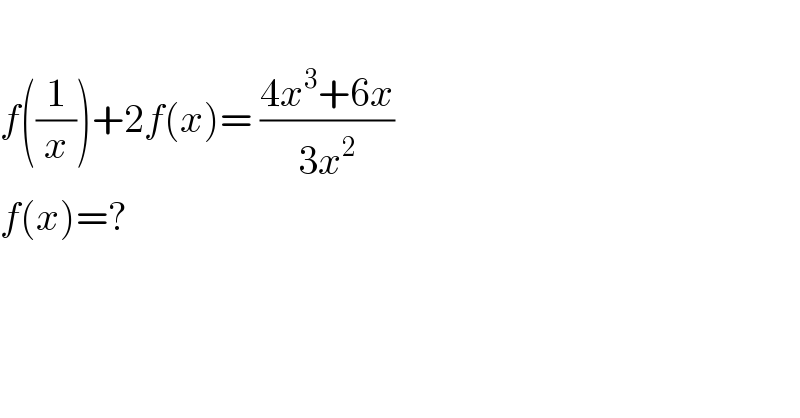
$$ \\ $$$${f}\left(\frac{\mathrm{1}}{{x}}\right)+\mathrm{2}{f}\left({x}\right)=\:\frac{\mathrm{4}{x}^{\mathrm{3}} +\mathrm{6}{x}}{\mathrm{3}{x}^{\mathrm{2}} } \\ $$$${f}\left({x}\right)=? \\ $$
Commented by john santu last updated on 01/May/20

$${replace}\:{x}\:{by}\:\frac{\mathrm{1}}{{x}} \\ $$$$\Rightarrow{f}\left({x}\right)+\mathrm{2}{f}\left(\frac{\mathrm{1}}{{x}}\right)=\:\frac{\left(\frac{\mathrm{4}}{{x}^{\mathrm{3}} }\right)+\left(\frac{\mathrm{6}}{{x}}\right)}{\left(\frac{\mathrm{3}}{{x}^{\mathrm{2}} }\right)} \\ $$$${f}\left({x}\right)+\mathrm{2}{f}\left(\frac{\mathrm{1}}{{x}}\right)\:=\:\frac{\mathrm{4}+\mathrm{6}{x}^{\mathrm{2}} }{\mathrm{3}{x}}…\left({ii}\right) \\ $$$$\left({i}\right)×\mathrm{2}\Rightarrow\:\mathrm{4}{f}\left({x}\right)+\mathrm{2}{f}\left(\frac{\mathrm{1}}{{x}}\right)=\frac{\mathrm{8}{x}^{\mathrm{3}} +\mathrm{12}{x}}{\mathrm{3}{x}^{\mathrm{2}} } \\ $$$$\left({i}\right)−\left({ii}\right) \\ $$$$\mathrm{3}{f}\left({x}\right)\:=\:\frac{\mathrm{8}{x}^{\mathrm{3}} +\mathrm{12}{x}}{\mathrm{3}{x}^{\mathrm{2}} }−\frac{\mathrm{6}{x}^{\mathrm{3}} +\mathrm{4}{x}}{\mathrm{3}{x}^{\mathrm{2}} } \\ $$$$\mathrm{3}{f}\left({x}\right)\:=\:\frac{\mathrm{2}{x}^{\mathrm{3}} +\mathrm{8}{x}}{\mathrm{3}{x}^{\mathrm{2}} }=\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{8}}{\mathrm{3}{x}} \\ $$$$\therefore{f}\left({x}\right)=\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{8}}{\mathrm{9}{x}} \\ $$
Commented by jagoll last updated on 01/May/20

$${thank}\:{you} \\ $$
