Question Number 119808 by Khalmohmmad last updated on 27/Oct/20
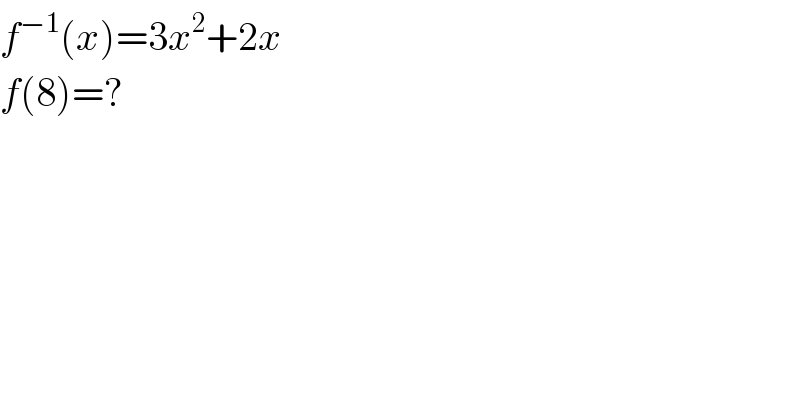
$${f}^{−\mathrm{1}} \left({x}\right)=\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x} \\ $$$${f}\left(\mathrm{8}\right)=? \\ $$
Answered by Ar Brandon last updated on 27/Oct/20
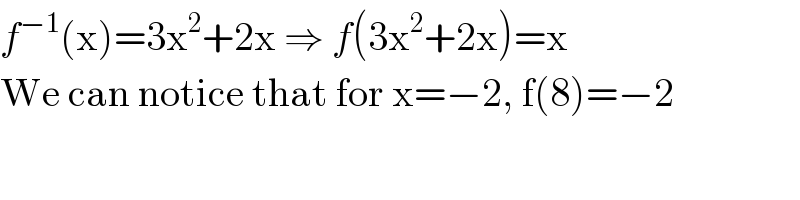
$${f}^{−\mathrm{1}} \left(\mathrm{x}\right)=\mathrm{3x}^{\mathrm{2}} +\mathrm{2x}\:\Rightarrow\:{f}\left(\mathrm{3x}^{\mathrm{2}} +\mathrm{2x}\right)=\mathrm{x} \\ $$$$\mathrm{We}\:\mathrm{can}\:\mathrm{notice}\:\mathrm{that}\:\mathrm{for}\:\mathrm{x}=−\mathrm{2},\:\mathrm{f}\left(\mathrm{8}\right)=−\mathrm{2} \\ $$
Answered by Dwaipayan Shikari last updated on 27/Oct/20
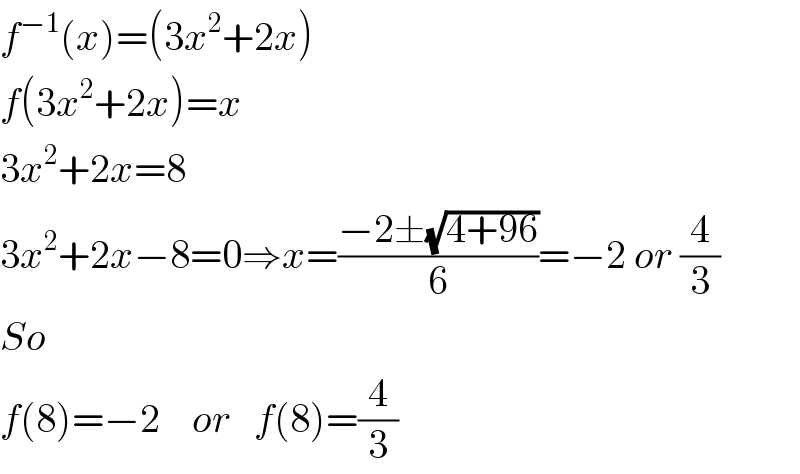
$${f}^{−\mathrm{1}} \left({x}\right)=\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}\right) \\ $$$${f}\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}\right)={x} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}=\mathrm{8} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{8}=\mathrm{0}\Rightarrow{x}=\frac{−\mathrm{2}\pm\sqrt{\mathrm{4}+\mathrm{96}}}{\mathrm{6}}=−\mathrm{2}\:{or}\:\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${So} \\ $$$${f}\left(\mathrm{8}\right)=−\mathrm{2}\:\:\:\:{or}\:\:\:{f}\left(\mathrm{8}\right)=\frac{\mathrm{4}}{\mathrm{3}} \\ $$
