Question Number 115960 by Fikret last updated on 29/Sep/20
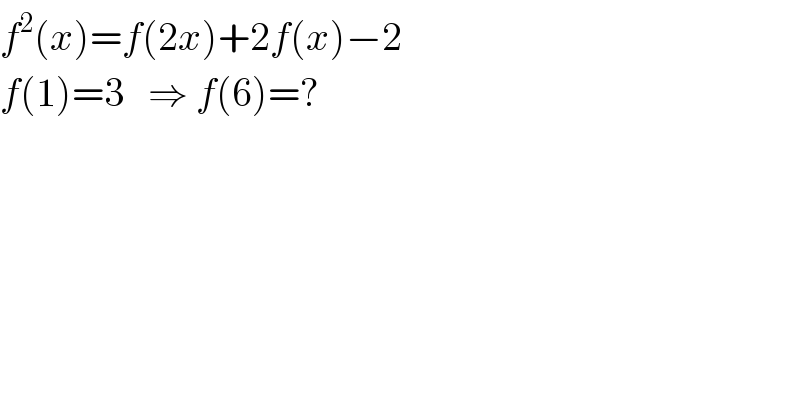
$${f}^{\mathrm{2}} \left({x}\right)={f}\left(\mathrm{2}{x}\right)+\mathrm{2}{f}\left({x}\right)−\mathrm{2}\: \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{3}\:\:\:\Rightarrow\:{f}\left(\mathrm{6}\right)=? \\ $$
Commented by prakash jain last updated on 29/Sep/20
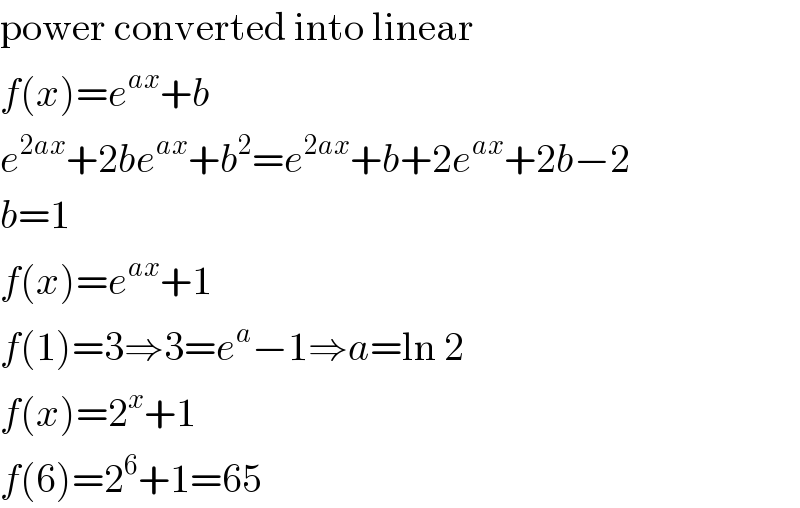
$$\mathrm{power}\:\mathrm{converted}\:\mathrm{into}\:\mathrm{linear} \\ $$$${f}\left({x}\right)={e}^{{ax}} +{b} \\ $$$${e}^{\mathrm{2}{ax}} +\mathrm{2}{be}^{{ax}} +{b}^{\mathrm{2}} ={e}^{\mathrm{2}{ax}} +{b}+\mathrm{2}{e}^{{ax}} +\mathrm{2}{b}−\mathrm{2} \\ $$$${b}=\mathrm{1} \\ $$$${f}\left({x}\right)={e}^{{ax}} +\mathrm{1} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{3}\Rightarrow\mathrm{3}={e}^{{a}} −\mathrm{1}\Rightarrow{a}=\mathrm{ln}\:\mathrm{2} \\ $$$${f}\left({x}\right)=\mathrm{2}^{{x}} +\mathrm{1} \\ $$$${f}\left(\mathrm{6}\right)=\mathrm{2}^{\mathrm{6}} +\mathrm{1}=\mathrm{65} \\ $$
