Question Number 164770 by cortano1 last updated on 21/Jan/22
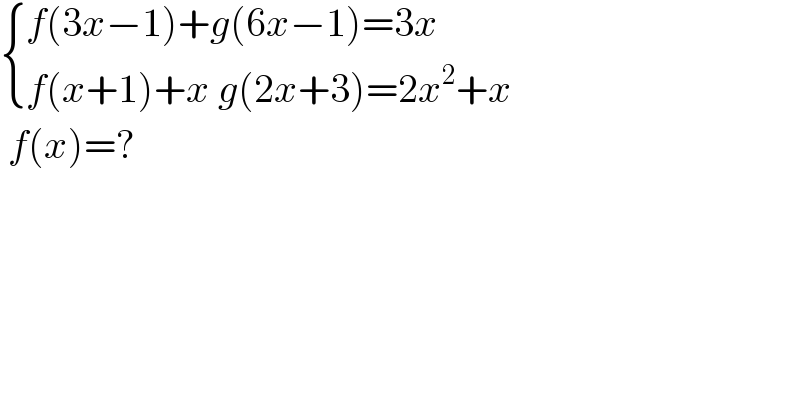
$$\begin{cases}{{f}\left(\mathrm{3}{x}−\mathrm{1}\right)+{g}\left(\mathrm{6}{x}−\mathrm{1}\right)=\mathrm{3}{x}}\\{{f}\left({x}+\mathrm{1}\right)+{x}\:{g}\left(\mathrm{2}{x}+\mathrm{3}\right)=\mathrm{2}{x}^{\mathrm{2}} +{x}}\end{cases} \\ $$$$\:{f}\left({x}\right)=? \\ $$
Answered by blackmamba last updated on 21/Jan/22

$$\:\mathrm{let}\:\begin{cases}{{f}\left({x}\right)={px}+{q}}\\{{g}\left({x}\right)={ax}+{b}}\end{cases} \\ $$$$\:\begin{cases}{{f}\left(\mathrm{3}{x}−\mathrm{1}\right)=\mathrm{3}{px}+{q}−{p}}\\{{g}\left(\mathrm{6}{x}−\mathrm{1}\right)=\mathrm{6}{ax}+{b}−{a}}\end{cases}\:\Rightarrow\left(\mathrm{3}{p}+\mathrm{6}{a}\right){x}+{b}+{q}−\left({a}+{p}\right)=\mathrm{3}{x} \\ $$$$\:\begin{cases}{\mathrm{3}{p}+\mathrm{6}{a}=\mathrm{3}}\\{{b}+{q}={a}+{p}\:}\end{cases} \\ $$$$\begin{cases}{{f}\left({x}+\mathrm{1}\right)={px}+{q}+{p}}\\{{g}\left(\mathrm{2}{x}+\mathrm{3}\right)=\mathrm{2}{ax}+{b}+\mathrm{3}{a}}\end{cases} \\ $$$$\:\Rightarrow{px}+{q}+{p}+\mathrm{2}{ax}^{\mathrm{2}} +\left({b}+\mathrm{3}{a}\right){x}=\mathrm{2}{x}^{\mathrm{2}} +{x} \\ $$$$\Rightarrow\mathrm{2}{ax}^{\mathrm{2}} +\left({b}+\mathrm{3}{a}+{p}\right){x}+{p}+{q}=\mathrm{2}{x}^{\mathrm{2}} +{x} \\ $$$$\:\begin{cases}{{p}+{q}=\mathrm{0}\Rightarrow{p}=−{q}}\\{\mathrm{2}{a}=\mathrm{2}\Rightarrow{a}=\mathrm{1}\:;\:{b}+\mathrm{3}{a}+{p}=\mathrm{1}\:;\:{b}+{p}=−\mathrm{2}}\end{cases} \\ $$$$\:\begin{cases}{\mathrm{3}{p}+\mathrm{6}\:=\mathrm{3}\Rightarrow{p}=−\mathrm{1}\:\wedge\:{q}=\mathrm{1}}\\{{b}+\mathrm{1}=\mathrm{1}+\left(−\mathrm{1}\right)\Rightarrow{b}=−\mathrm{1}}\end{cases} \\ $$$$\:\therefore\:\begin{cases}{{f}\left({x}\right)=−{x}+\mathrm{1}}\\{{g}\left({x}\right)=\:{x}−\mathrm{1}}\end{cases} \\ $$
Answered by TheSupreme last updated on 21/Jan/22
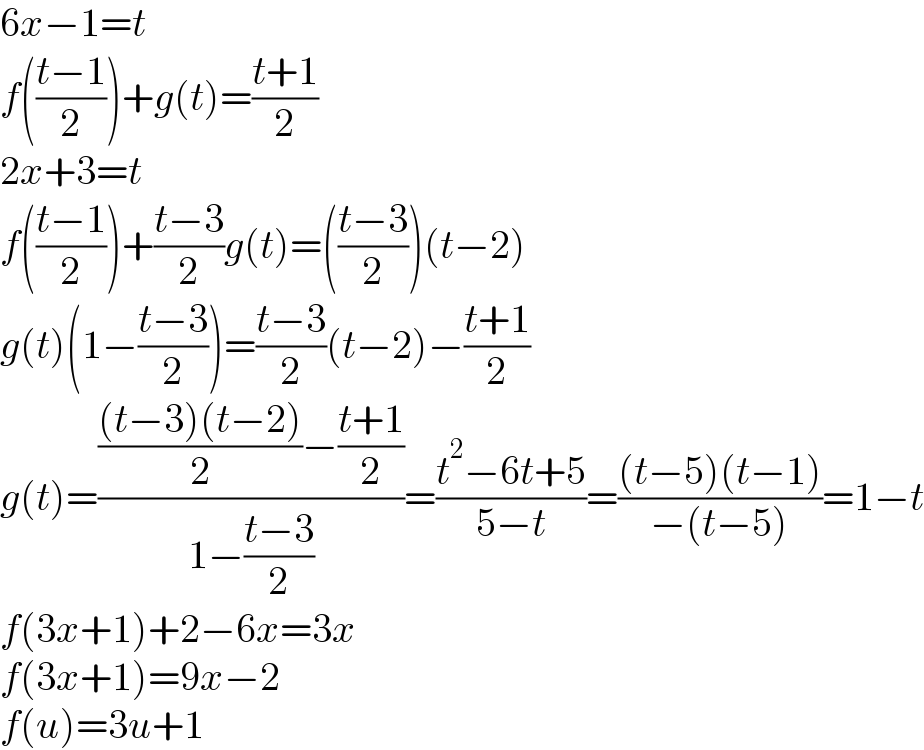
$$\mathrm{6}{x}−\mathrm{1}={t} \\ $$$${f}\left(\frac{{t}−\mathrm{1}}{\mathrm{2}}\right)+{g}\left({t}\right)=\frac{{t}+\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{2}{x}+\mathrm{3}={t} \\ $$$${f}\left(\frac{{t}−\mathrm{1}}{\mathrm{2}}\right)+\frac{{t}−\mathrm{3}}{\mathrm{2}}{g}\left({t}\right)=\left(\frac{{t}−\mathrm{3}}{\mathrm{2}}\right)\left({t}−\mathrm{2}\right) \\ $$$${g}\left({t}\right)\left(\mathrm{1}−\frac{{t}−\mathrm{3}}{\mathrm{2}}\right)=\frac{{t}−\mathrm{3}}{\mathrm{2}}\left({t}−\mathrm{2}\right)−\frac{{t}+\mathrm{1}}{\mathrm{2}} \\ $$$${g}\left({t}\right)=\frac{\frac{\left({t}−\mathrm{3}\right)\left({t}−\mathrm{2}\right)}{\mathrm{2}}−\frac{{t}+\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\frac{{t}−\mathrm{3}}{\mathrm{2}}}=\frac{{t}^{\mathrm{2}} −\mathrm{6}{t}+\mathrm{5}}{\mathrm{5}−{t}}=\frac{\left({t}−\mathrm{5}\right)\left({t}−\mathrm{1}\right)}{−\left({t}−\mathrm{5}\right)}=\mathrm{1}−{t} \\ $$$${f}\left(\mathrm{3}{x}+\mathrm{1}\right)+\mathrm{2}−\mathrm{6}{x}=\mathrm{3}{x} \\ $$$${f}\left(\mathrm{3}{x}+\mathrm{1}\right)=\mathrm{9}{x}−\mathrm{2} \\ $$$${f}\left({u}\right)=\mathrm{3}{u}+\mathrm{1} \\ $$
