Question Number 161516 by naka3546 last updated on 19/Dec/21

$${f}'\left({a}\right)\:\:{is}\:\:{derivative}\:\:{of}\:\:{function}\:\:{f}\left({a}\right)\:. \\ $$$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{{f}\left({a}−\mathrm{2}{h}^{\mathrm{2}} \right)−{f}\left({a}+{h}^{\mathrm{3}} \right)}{{h}^{\mathrm{2}} }\:\:=\:\:? \\ $$
Commented by cortano last updated on 19/Dec/21

$$\:=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{4}{hf}\:'\left({a}−\mathrm{2}{h}^{\mathrm{2}} \right)−\mathrm{3}{h}^{\mathrm{2}} {f}\:'\left({a}+{h}^{\mathrm{3}} \right)}{\mathrm{2}{h}} \\ $$$$\:=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{4}{f}\:'\left({a}−\mathrm{2}{h}^{\mathrm{2}} \right)−\mathrm{3}{hf}\:'\left({a}+{h}^{\mathrm{3}} \right)}{\mathrm{2}} \\ $$$$\:=\:−\mathrm{2}{f}\:'\left({a}\right) \\ $$
Commented by naka3546 last updated on 19/Dec/21
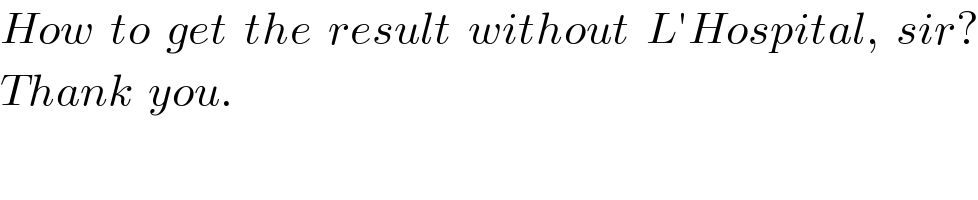
$${How}\:\:{to}\:\:{get}\:\:{the}\:\:{result}\:\:{without}\:\:{L}'{Hospital},\:\:{sir}? \\ $$$${Thank}\:\:{you}. \\ $$
