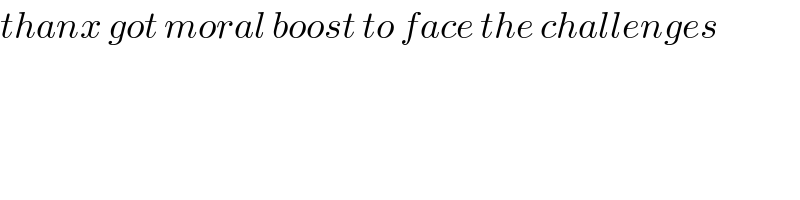Question Number 37840 by ajfour last updated on 18/Jun/18
![f(θ,φ)=((cos φ[cos θ tan (((θ+φ)/2))−sin θ]^2 )/(cos φtan (((θ+φ)/2))+sin φ)) φ ∈ (0,(π/2)) , θ ∈ (−(π/2), (π/2)); find maximum f(θ,φ).](https://www.tinkutara.com/question/Q37840.png)
$${f}\left(\theta,\phi\right)=\frac{\mathrm{cos}\:\phi\left[\mathrm{cos}\:\theta\:\mathrm{tan}\:\left(\frac{\theta+\phi}{\mathrm{2}}\right)−\mathrm{sin}\:\theta\right]^{\mathrm{2}} }{\mathrm{cos}\:\phi\mathrm{tan}\:\left(\frac{\theta+\phi}{\mathrm{2}}\right)+\mathrm{sin}\:\phi} \\ $$$$\:\phi\:\in\:\left(\mathrm{0},\frac{\pi}{\mathrm{2}}\right)\:,\:\theta\:\in\:\left(−\frac{\pi}{\mathrm{2}},\:\frac{\pi}{\mathrm{2}}\right); \\ $$$${find}\:{maximum}\:{f}\left(\theta,\phi\right). \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Jun/18
![f(θ,φ)=(N_r /D_r ) N_r =cosφ[cosθtan(((θ+φ)/2))−sinθ]^2 =cosφ[((cosθsin(((θ+φ)/2))−sinθcos(((θ+φ)/2)))/(cos(((θ+∅)/2))))]^2 =cosφ[((sin(((φ−θ)/2)))/(cos(((θ+φ)/2))))]^2 D_r =cosφtan(((θ+φ)/2))+sinφ =((cosφ.sin(((θ+φ)/2))+cos(((θ+φ)/2))sinφ)/(cos(((θ+∅)/2)))) =((sin(((θ+3φ)/2)))/(cos(((θ+φ)/2)))) f(θ,φ)=((cosφ[sin(((φ−θ)/2))]^2 ×cos(((θ+φ)/2)))/(sin(((θ+3φ)/2))×[cos(((θ+φ)/2)]^2 )) =((cosφ[sin(((φ−θ)/2))]^2 )/(sin(((θ+3φ)/2))cos(((θ+φ)/2)))) =((2cosφ[sin(((φ−θ)/2))]^2 )/(2sin(φ+((θ+∅)/2))cos(((θ+φ)/2))))=((2cos0[sin^2 (−(Π/4))})/(2sin(Π/4)×cos(Π/4)))=1 wait... φ (0,(Π/2)) θ(((−Π)/2),(Π/2)) max N_r when φ=0 θ=(Π/2)](https://www.tinkutara.com/question/Q37846.png)
$${f}\left(\theta,\phi\right)=\frac{{N}_{{r}} }{{D}_{{r}} } \\ $$$${N}_{{r}} ={cos}\phi\left[{cos}\theta{tan}\left(\frac{\theta+\phi}{\mathrm{2}}\right)−{sin}\theta\right]^{\mathrm{2}} \\ $$$$={cos}\phi\left[\frac{{cos}\theta{sin}\left(\frac{\theta+\phi}{\mathrm{2}}\right)−{sin}\theta{cos}\left(\frac{\theta+\phi}{\mathrm{2}}\right)}{{cos}\left(\frac{\theta+\emptyset}{\mathrm{2}}\right)}\right]^{\mathrm{2}} \\ $$$$={cos}\phi\left[\frac{{sin}\left(\frac{\phi−\theta}{\mathrm{2}}\right)}{{cos}\left(\frac{\theta+\phi}{\mathrm{2}}\right)}\right]^{\mathrm{2}} \\ $$$${D}_{{r}} ={cos}\phi{tan}\left(\frac{\theta+\phi}{\mathrm{2}}\right)+{sin}\phi \\ $$$$=\frac{{cos}\phi.{sin}\left(\frac{\theta+\phi}{\mathrm{2}}\right)+{cos}\left(\frac{\theta+\phi}{\mathrm{2}}\right){sin}\phi}{{cos}\left(\frac{\theta+\emptyset}{\mathrm{2}}\right)} \\ $$$$=\frac{{sin}\left(\frac{\theta+\mathrm{3}\phi}{\mathrm{2}}\right)}{{cos}\left(\frac{\theta+\phi}{\mathrm{2}}\right)} \\ $$$${f}\left(\theta,\phi\right)=\frac{{cos}\phi\left[{sin}\left(\frac{\phi−\theta}{\mathrm{2}}\right)\right]^{\mathrm{2}} ×{cos}\left(\frac{\theta+\phi}{\mathrm{2}}\right)}{{sin}\left(\frac{\theta+\mathrm{3}\phi}{\mathrm{2}}\right)×\left[{cos}\frac{\left(\theta+\phi\right.}{\mathrm{2}}\right]^{\mathrm{2}} } \\ $$$$=\frac{{cos}\phi\left[{sin}\left(\frac{\phi−\theta}{\mathrm{2}}\right)\right]^{\mathrm{2}} }{{sin}\left(\frac{\theta+\mathrm{3}\phi}{\mathrm{2}}\right){cos}\left(\frac{\theta+\phi}{\mathrm{2}}\right)}\:\:\: \\ $$$$=\frac{\mathrm{2}{cos}\phi\left[{sin}\left(\frac{\phi−\theta}{\mathrm{2}}\right)\right]^{\mathrm{2}} }{\mathrm{2}{sin}\left(\phi+\frac{\theta+\emptyset}{\mathrm{2}}\right){cos}\left(\frac{\theta+\phi}{\mathrm{2}}\right)}=\frac{\mathrm{2}{cos}\mathrm{0}\left[{sin}^{\mathrm{2}} \left(−\frac{\Pi}{\mathrm{4}}\right)\right\}}{\mathrm{2}{sin}\frac{\Pi}{\mathrm{4}}×{cos}\frac{\Pi}{\mathrm{4}}}=\mathrm{1} \\ $$$${wait}…\:\phi\:\left(\mathrm{0},\frac{\Pi}{\mathrm{2}}\right)\:\:\:\:\theta\left(\frac{−\Pi}{\mathrm{2}},\frac{\Pi}{\mathrm{2}}\right) \\ $$$${max}\:{N}_{{r}} \:{when}\:\phi=\mathrm{0}\:\:\:\theta=\frac{\Pi}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$
Commented by ajfour last updated on 18/Jun/18
![i should have given θ,φ ∈[−(π/2),(π/2)]. Thank you Tanmay Sir. Your answer is indeed right, i believe.](https://www.tinkutara.com/question/Q37853.png)
$${i}\:{should}\:{have}\:{given}\:\theta,\phi\:\in\left[−\frac{\pi}{\mathrm{2}},\frac{\pi}{\mathrm{2}}\right]. \\ $$$${Thank}\:{you}\:{Tanmay}\:{Sir}. \\ $$$${Your}\:{answer}\:{is}\:{indeed}\:{right}, \\ $$$${i}\:{believe}.\: \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 18/Jun/18
$${thanx}\:{got}\:{moral}\:{boost}\:{to}\:{face}\:{the}\:{challenges} \\ $$