Question Number 32743 by naka3546 last updated on 01/Apr/18

$${f}\:\left({f}\:\left({n}\right)\right)\:\:=\:\:\mathrm{2}{n} \\ $$$${f}\:\left({n}\right)\:\:=\:\:? \\ $$
Commented by abdo imad last updated on 03/Apr/18
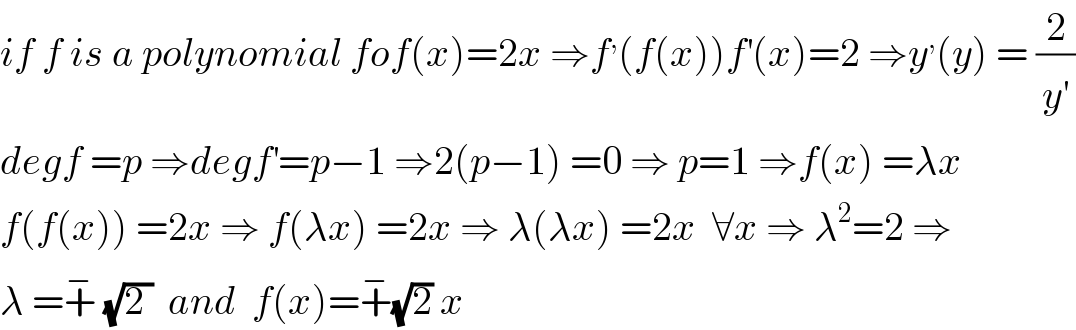
$${if}\:{f}\:{is}\:{a}\:{polynomial}\:{fof}\left({x}\right)=\mathrm{2}{x}\:\Rightarrow{f}^{,} \left({f}\left({x}\right)\right){f}^{'} \left({x}\right)=\mathrm{2}\:\Rightarrow{y}^{,} \left({y}\right)\:=\:\frac{\mathrm{2}}{{y}^{'} } \\ $$$${degf}\:={p}\:\Rightarrow{degf}^{'} ={p}−\mathrm{1}\:\Rightarrow\mathrm{2}\left({p}−\mathrm{1}\right)\:=\mathrm{0}\:\Rightarrow\:{p}=\mathrm{1}\:\Rightarrow{f}\left({x}\right)\:=\lambda{x} \\ $$$${f}\left({f}\left({x}\right)\right)\:=\mathrm{2}{x}\:\Rightarrow\:{f}\left(\lambda{x}\right)\:=\mathrm{2}{x}\:\Rightarrow\:\lambda\left(\lambda{x}\right)\:=\mathrm{2}{x}\:\:\forall{x}\:\Rightarrow\:\lambda^{\mathrm{2}} =\mathrm{2}\:\Rightarrow \\ $$$$\lambda\:=\overset{−} {+}\:\sqrt{\mathrm{2}\:}\:\:{and}\:\:{f}\left({x}\right)=\overset{−} {+}\sqrt{\mathrm{2}}\:{x} \\ $$
Answered by Joel578 last updated on 02/Apr/18
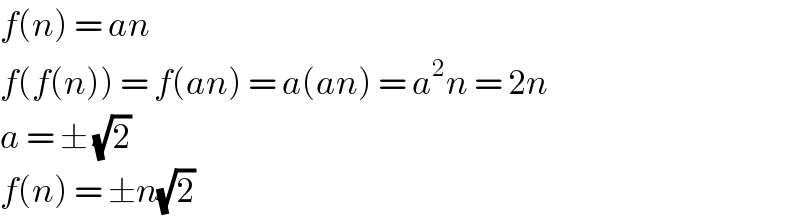
$${f}\left({n}\right)\:=\:{an} \\ $$$${f}\left({f}\left({n}\right)\right)\:=\:{f}\left({an}\right)\:=\:{a}\left({an}\right)\:=\:{a}^{\mathrm{2}} {n}\:=\:\mathrm{2}{n} \\ $$$${a}\:=\:\pm\:\sqrt{\mathrm{2}} \\ $$$${f}\left({n}\right)\:=\:\pm{n}\sqrt{\mathrm{2}} \\ $$
Answered by MJS last updated on 01/Apr/18

$${f}\left({n}\right)=\pm{n}\sqrt{\mathrm{2}} \\ $$
