Question Number 158668 by cortano last updated on 07/Nov/21
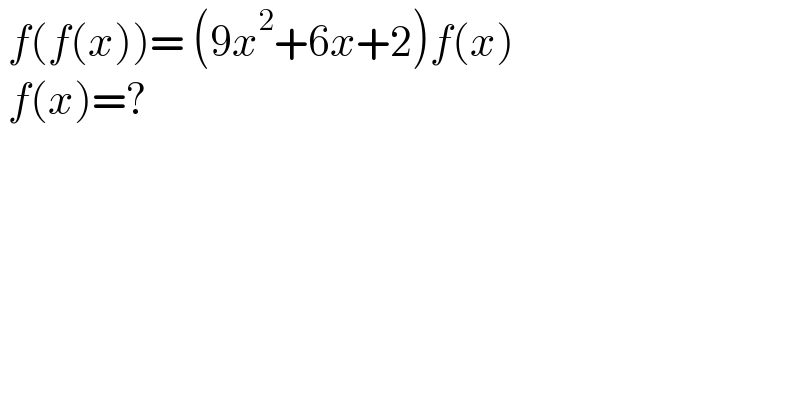
$$\:{f}\left({f}\left({x}\right)\right)=\:\left(\mathrm{9}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{2}\right){f}\left({x}\right) \\ $$$$\:{f}\left({x}\right)=? \\ $$
Answered by ajfour last updated on 07/Nov/21
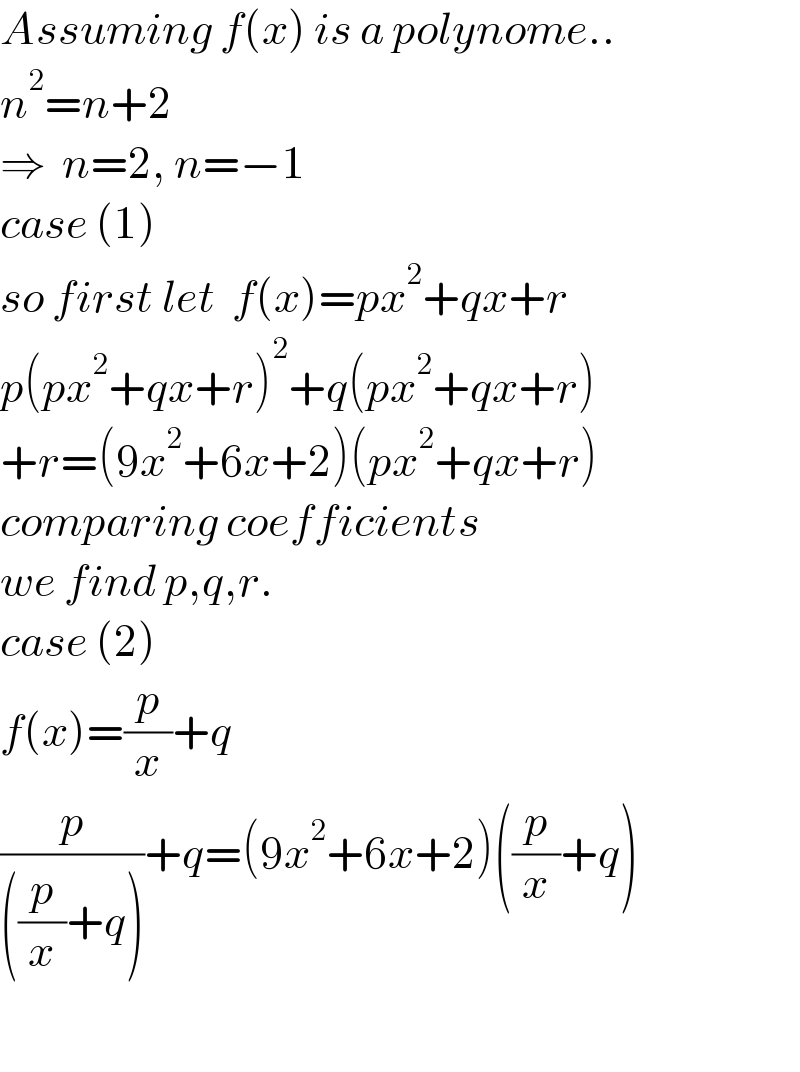
$${Assuming}\:{f}\left({x}\right)\:{is}\:{a}\:{polynome}.. \\ $$$${n}^{\mathrm{2}} ={n}+\mathrm{2} \\ $$$$\Rightarrow\:\:{n}=\mathrm{2},\:{n}=−\mathrm{1} \\ $$$${case}\:\left(\mathrm{1}\right) \\ $$$${so}\:{first}\:{let}\:\:{f}\left({x}\right)={px}^{\mathrm{2}} +{qx}+{r} \\ $$$${p}\left({px}^{\mathrm{2}} +{qx}+{r}\right)^{\mathrm{2}} +{q}\left({px}^{\mathrm{2}} +{qx}+{r}\right) \\ $$$$+{r}=\left(\mathrm{9}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{2}\right)\left({px}^{\mathrm{2}} +{qx}+{r}\right) \\ $$$${comparing}\:{coefficients} \\ $$$${we}\:{find}\:{p},{q},{r}. \\ $$$${case}\:\left(\mathrm{2}\right) \\ $$$${f}\left({x}\right)=\frac{{p}}{{x}}+{q} \\ $$$$\frac{{p}}{\left(\frac{{p}}{{x}}+{q}\right)}+{q}=\left(\mathrm{9}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{2}\right)\left(\frac{{p}}{{x}}+{q}\right) \\ $$$$ \\ $$
