Question Number 99919 by abdomathmax last updated on 24/Jun/20
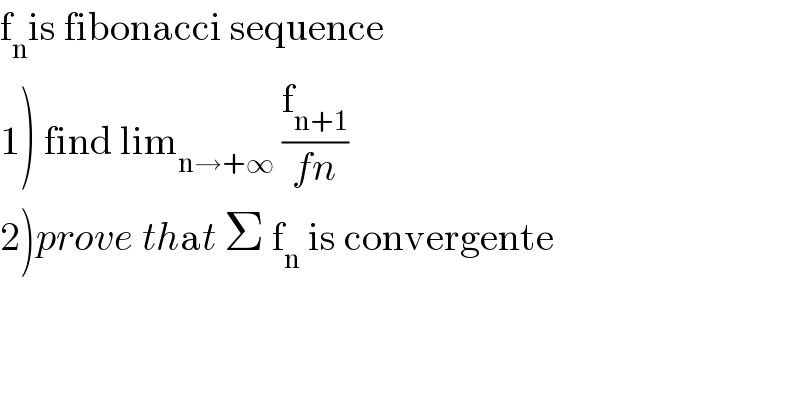
$$\mathrm{f}_{\mathrm{n}} \mathrm{is}\:\mathrm{fibonacci}\:\mathrm{sequence} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{find}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\frac{\mathrm{f}_{\mathrm{n}+\mathrm{1}} }{{fn}} \\ $$$$\left.\mathrm{2}\right){prove}\:{th}\mathrm{a}{t}\:\Sigma\:\mathrm{f}_{\mathrm{n}} \:\mathrm{is}\:\mathrm{convergente} \\ $$
Answered by abdomathmax last updated on 24/Jun/20
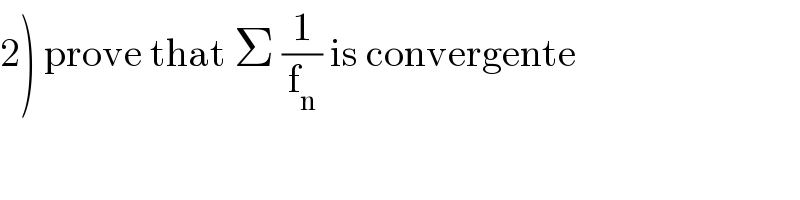
$$\left.\mathrm{2}\right)\:\mathrm{prove}\:\mathrm{that}\:\Sigma\:\frac{\mathrm{1}}{\mathrm{f}_{\mathrm{n}} }\:\mathrm{is}\:\mathrm{convergente} \\ $$
