Question Number 128485 by BHOOPENDRA last updated on 07/Jan/21

$${f}\left({t}\right)=\frac{\mathrm{1}−{cos}\mathrm{2}{t}}{{t}} \\ $$$${find}\:{laplace}\:{transformation}? \\ $$
Answered by Dwaipayan Shikari last updated on 07/Jan/21
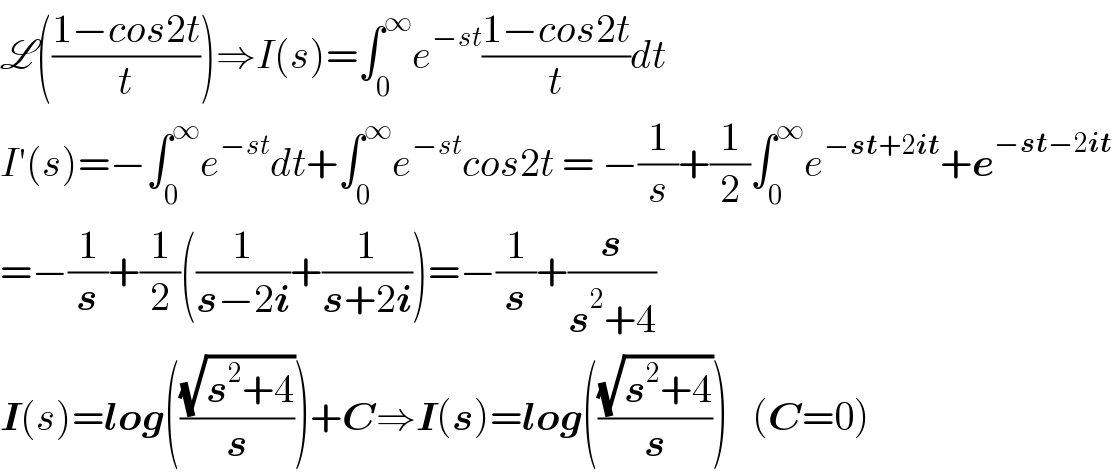
$$\mathscr{L}\left(\frac{\mathrm{1}−{cos}\mathrm{2}{t}}{{t}}\right)\Rightarrow{I}\left({s}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{st}} \frac{\mathrm{1}−{cos}\mathrm{2}{t}}{{t}}{dt} \\ $$$${I}'\left({s}\right)=−\int_{\mathrm{0}} ^{\infty} {e}^{−{st}} {dt}+\int_{\mathrm{0}} ^{\infty} {e}^{−{st}} {cos}\mathrm{2}{t}\:=\:−\frac{\mathrm{1}}{{s}}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {e}^{−\boldsymbol{{st}}+\mathrm{2}\boldsymbol{{it}}} +\boldsymbol{{e}}^{−\boldsymbol{{st}}−\mathrm{2}\boldsymbol{{it}}} \\ $$$$=−\frac{\mathrm{1}}{\boldsymbol{{s}}}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\boldsymbol{{s}}−\mathrm{2}\boldsymbol{{i}}}+\frac{\mathrm{1}}{\boldsymbol{{s}}+\mathrm{2}\boldsymbol{{i}}}\right)=−\frac{\mathrm{1}}{\boldsymbol{{s}}}+\frac{\boldsymbol{{s}}}{\boldsymbol{{s}}^{\mathrm{2}} +\mathrm{4}} \\ $$$$\boldsymbol{{I}}\left({s}\right)=\boldsymbol{{log}}\left(\frac{\sqrt{\boldsymbol{{s}}^{\mathrm{2}} +\mathrm{4}}}{\boldsymbol{{s}}}\right)+\boldsymbol{{C}}\Rightarrow\boldsymbol{{I}}\left(\boldsymbol{{s}}\right)=\boldsymbol{{log}}\left(\frac{\sqrt{\boldsymbol{{s}}^{\mathrm{2}} +\mathrm{4}}}{\boldsymbol{{s}}}\right)\:\:\:\left(\boldsymbol{{C}}=\mathrm{0}\right) \\ $$
Commented by BHOOPENDRA last updated on 07/Jan/21

$${thanks}\:{sir} \\ $$
