Question Number 161590 by geron last updated on 20/Dec/21
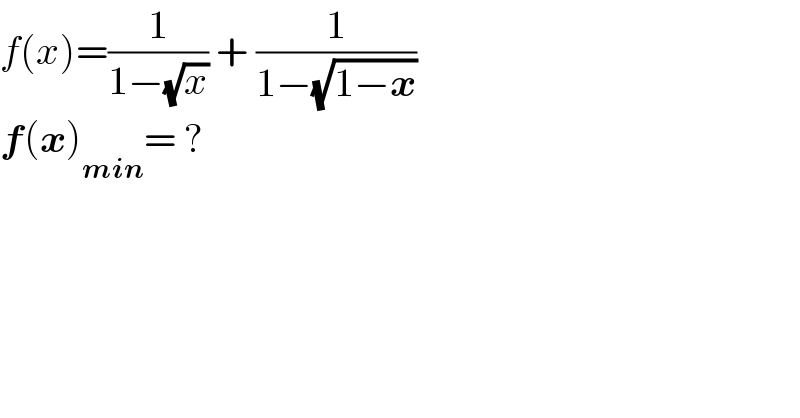
$${f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}−\sqrt{{x}}}\:+\:\frac{\mathrm{1}}{\mathrm{1}−\sqrt{\mathrm{1}−\boldsymbol{{x}}}} \\ $$$$\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)_{\boldsymbol{{min}}} =\:? \\ $$
Answered by cortano last updated on 20/Dec/21

Answered by mr W last updated on 20/Dec/21
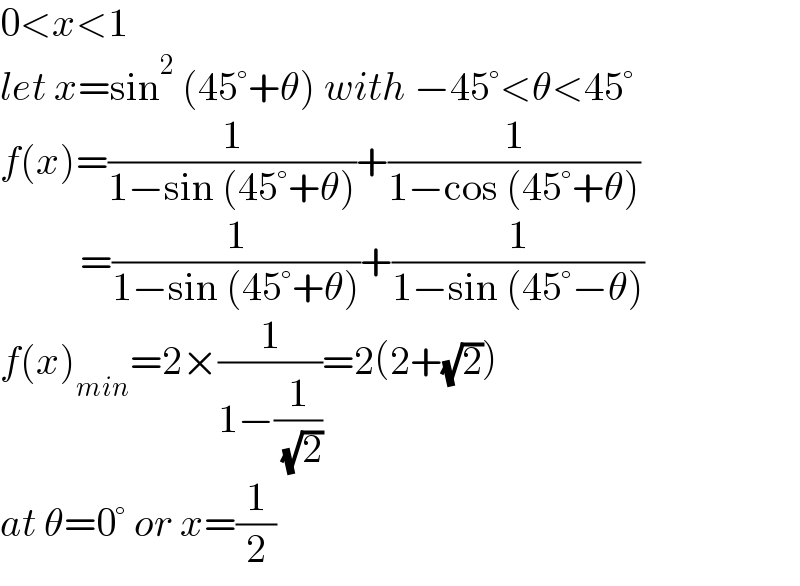
$$\mathrm{0}<{x}<\mathrm{1} \\ $$$${let}\:{x}=\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{45}°+\theta\right)\:{with}\:−\mathrm{45}°<\theta<\mathrm{45}° \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}\:\left(\mathrm{45}°+\theta\right)}+\frac{\mathrm{1}}{\mathrm{1}−\mathrm{cos}\:\left(\mathrm{45}°+\theta\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}\:\left(\mathrm{45}°+\theta\right)}+\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}\:\left(\mathrm{45}°−\theta\right)} \\ $$$${f}\left({x}\right)_{{min}} =\mathrm{2}×\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}=\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right) \\ $$$${at}\:\theta=\mathrm{0}°\:{or}\:{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
