Question Number 158039 by HongKing last updated on 30/Oct/21
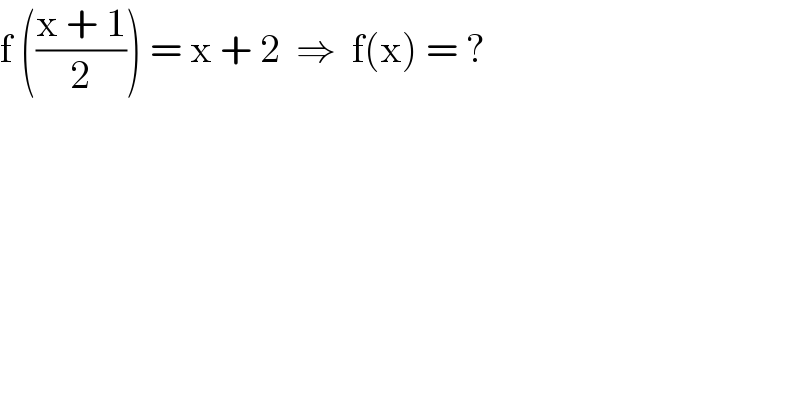
$$\mathrm{f}\:\left(\frac{\mathrm{x}\:+\:\mathrm{1}}{\mathrm{2}}\right)\:=\:\mathrm{x}\:+\:\mathrm{2}\:\:\Rightarrow\:\:\mathrm{f}\left(\mathrm{x}\right)\:=\:? \\ $$
Answered by puissant last updated on 30/Oct/21
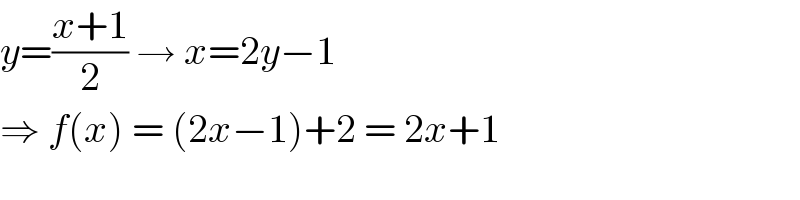
$${y}=\frac{{x}+\mathrm{1}}{\mathrm{2}}\:\rightarrow\:{x}=\mathrm{2}{y}−\mathrm{1} \\ $$$$\Rightarrow\:{f}\left({x}\right)\:=\:\left(\mathrm{2}{x}−\mathrm{1}\right)+\mathrm{2}\:=\:\mathrm{2}{x}+\mathrm{1} \\ $$
Answered by yeti123 last updated on 30/Oct/21
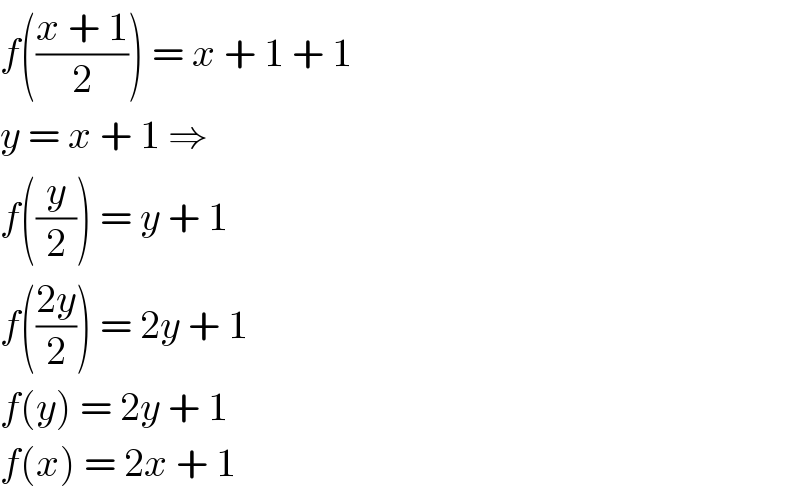
$${f}\left(\frac{{x}\:+\:\mathrm{1}}{\mathrm{2}}\right)\:=\:{x}\:+\:\mathrm{1}\:+\:\mathrm{1} \\ $$$${y}\:=\:{x}\:+\:\mathrm{1}\:\Rightarrow \\ $$$${f}\left(\frac{{y}}{\mathrm{2}}\right)\:=\:{y}\:+\:\mathrm{1} \\ $$$${f}\left(\frac{\mathrm{2}{y}}{\mathrm{2}}\right)\:=\:\mathrm{2}{y}\:+\:\mathrm{1} \\ $$$${f}\left({y}\right)\:=\:\mathrm{2}{y}\:+\:\mathrm{1} \\ $$$${f}\left({x}\right)\:=\:\mathrm{2}{x}\:+\:\mathrm{1} \\ $$
Commented by Rasheed.Sindhi last updated on 30/Oct/21
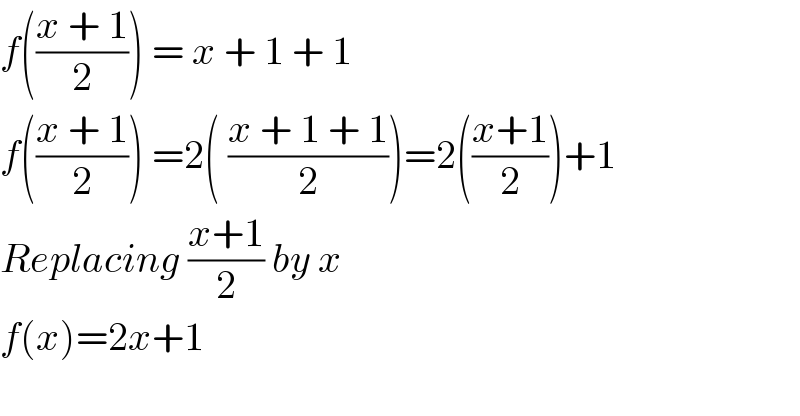
$${f}\left(\frac{{x}\:+\:\mathrm{1}}{\mathrm{2}}\right)\:=\:{x}\:+\:\mathrm{1}\:+\:\mathrm{1} \\ $$$${f}\left(\frac{{x}\:+\:\mathrm{1}}{\mathrm{2}}\right)\:=\mathrm{2}\left(\:\frac{{x}\:+\:\mathrm{1}\:+\:\mathrm{1}}{\mathrm{2}}\right)=\mathrm{2}\left(\frac{{x}+\mathrm{1}}{\mathrm{2}}\right)+\mathrm{1} \\ $$$${Replacing}\:\frac{{x}+\mathrm{1}}{\mathrm{2}}\:{by}\:{x} \\ $$$${f}\left({x}\right)=\mathrm{2}{x}+\mathrm{1} \\ $$$$ \\ $$
