Question Number 128156 by DomaPeti last updated on 04/Jan/21
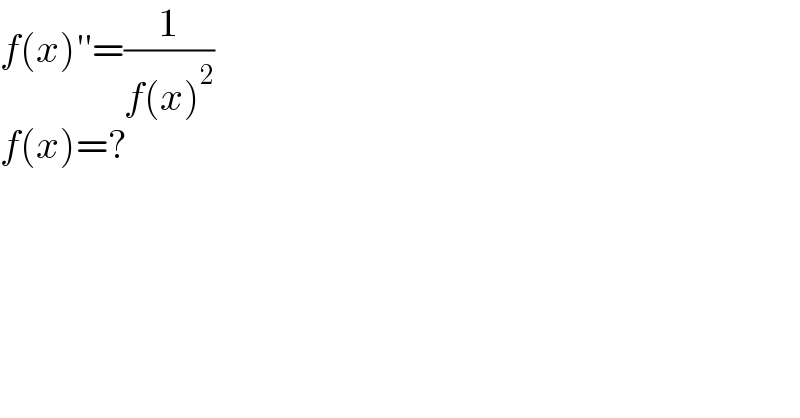
$${f}\left({x}\right)''=\frac{\mathrm{1}}{{f}\left({x}\right)^{\mathrm{2}} }\:\:\:\:\: \\ $$$${f}\left({x}\right)=? \\ $$
Answered by mr W last updated on 05/Jan/21
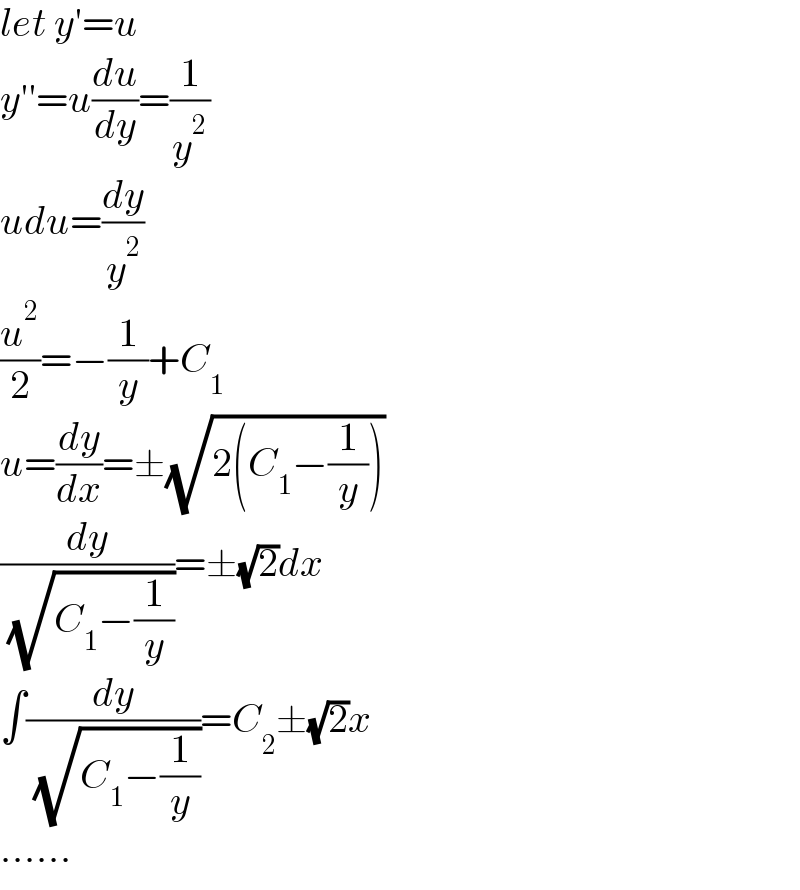
$${let}\:{y}'={u} \\ $$$${y}''={u}\frac{{du}}{{dy}}=\frac{\mathrm{1}}{{y}^{\mathrm{2}} } \\ $$$${udu}=\frac{{dy}}{{y}^{\mathrm{2}} } \\ $$$$\frac{{u}^{\mathrm{2}} }{\mathrm{2}}=−\frac{\mathrm{1}}{{y}}+{C}_{\mathrm{1}} \\ $$$${u}=\frac{{dy}}{{dx}}=\pm\sqrt{\mathrm{2}\left({C}_{\mathrm{1}} −\frac{\mathrm{1}}{{y}}\right)} \\ $$$$\frac{{dy}}{\:\sqrt{{C}_{\mathrm{1}} −\frac{\mathrm{1}}{{y}}}}=\pm\sqrt{\mathrm{2}}{dx} \\ $$$$\int\frac{{dy}}{\:\sqrt{{C}_{\mathrm{1}} −\frac{\mathrm{1}}{{y}}}}={C}_{\mathrm{2}} \pm\sqrt{\mathrm{2}}{x} \\ $$$$…… \\ $$
