f-x-1-x-2-x-2018-f-0-

Question Number 147402 by vvvv last updated on 20/Jul/21

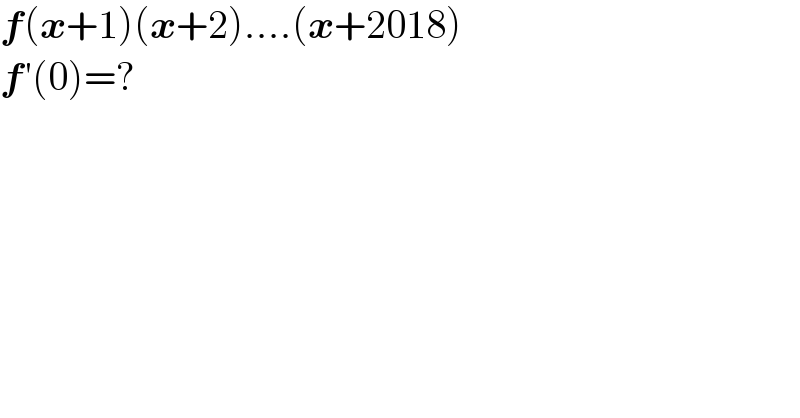
$$\boldsymbol{{f}}\left(\boldsymbol{{x}}+\mathrm{1}\right)\left(\boldsymbol{{x}}+\mathrm{2}\right)….\left(\boldsymbol{{x}}+\mathrm{2018}\right) \\ $$$$\boldsymbol{{f}}'\left(\mathrm{0}\right)=? \\ $$

Answered by SEKRET last updated on 21/Jul/21

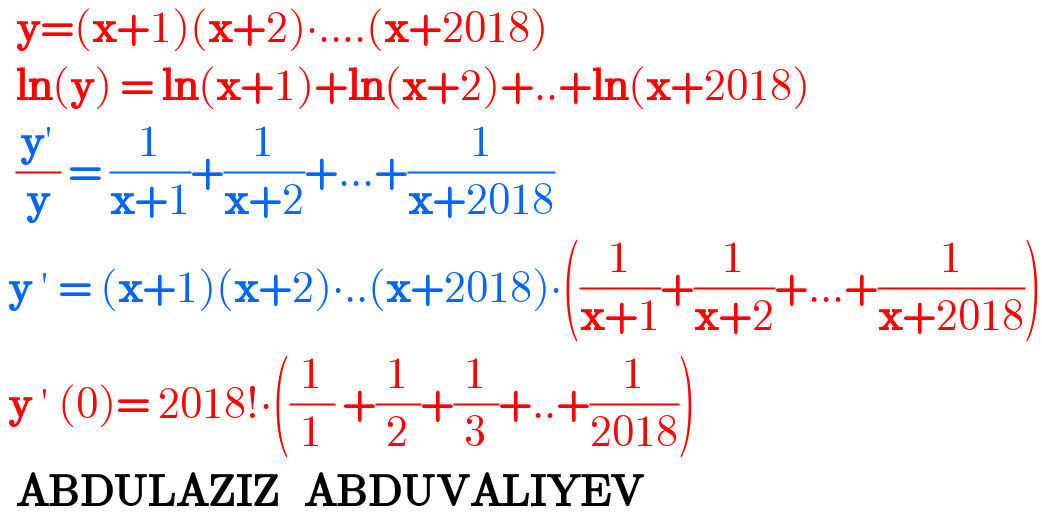
y=(x+1)(x+2)∙....(x+2018) ln(y) = ln(x+1)+ln(x+2)+..+ln(x+2018) ((y′)/y) = (1/(x+1))+(1/(x+2))+...+(1/(x+2018)) y ′ = (x+1)(x+2)∙..(x+2018)∙((1/(x+1))+(1/(x+2))+...+(1/(x+2018))) y ′ (0)= 2018!∙((1/1) +(1/2)+(1/3)+..+(1/(2018))) ABDULAZIZ ABDUVALIYEV

$$\:\:\boldsymbol{\mathrm{y}}=\left(\boldsymbol{\mathrm{x}}+\mathrm{1}\right)\left(\boldsymbol{\mathrm{x}}+\mathrm{2}\right)\centerdot….\left(\boldsymbol{\mathrm{x}}+\mathrm{2018}\right) \\ $$$$\:\:\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{y}}\right)\:=\:\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}+\mathrm{1}\right)+\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}+\mathrm{2}\right)+..+\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}+\mathrm{2018}\right) \\ $$$$\:\:\frac{\boldsymbol{\mathrm{y}}'}{\boldsymbol{\mathrm{y}}}\:=\:\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}+\mathrm{1}}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}+\mathrm{2}}+…+\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}+\mathrm{2018}} \\ $$$$\:\boldsymbol{\mathrm{y}}\:'\:=\:\left(\boldsymbol{\mathrm{x}}+\mathrm{1}\right)\left(\boldsymbol{\mathrm{x}}+\mathrm{2}\right)\centerdot..\left(\boldsymbol{\mathrm{x}}+\mathrm{2018}\right)\centerdot\left(\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}+\mathrm{1}}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}+\mathrm{2}}+…+\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}+\mathrm{2018}}\right) \\ $$$$\:\boldsymbol{\mathrm{y}}\:'\:\left(\mathrm{0}\right)=\:\mathrm{2018}!\centerdot\left(\frac{\mathrm{1}}{\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+..+\frac{\mathrm{1}}{\mathrm{2018}}\right) \\ $$$$\:\:\boldsymbol{\mathrm{ABDULAZIZ}}\:\:\:\boldsymbol{\mathrm{ABDUVALIYEV}}\: \\ $$

Answered by Olaf_Thorendsen last updated on 20/Jul/21

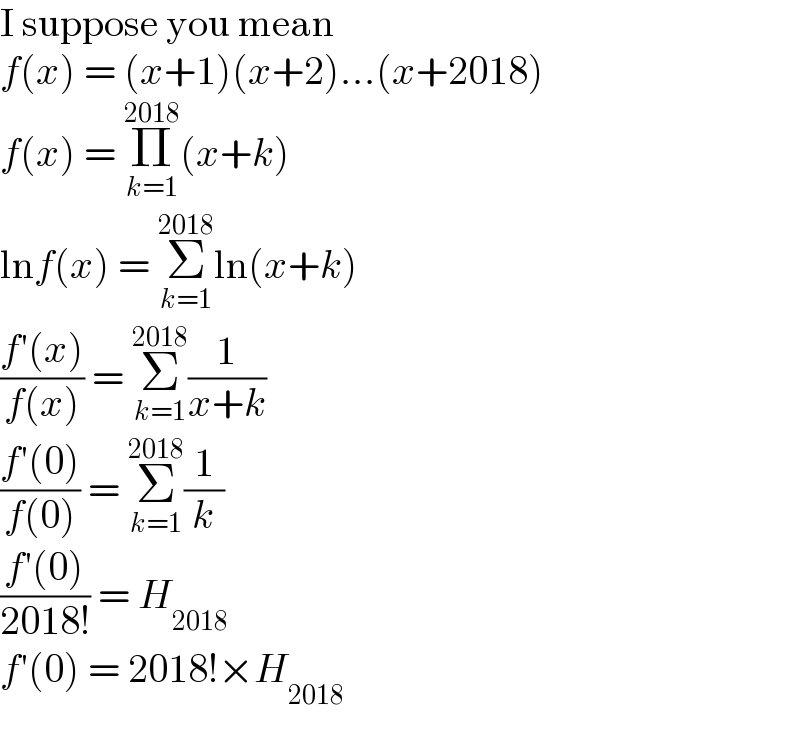
I suppose you mean f(x) = (x+1)(x+2)...(x+2018) f(x) = Π_(k=1) ^(2018) (x+k) lnf(x) = Σ_(k=1) ^(2018) ln(x+k) ((f′(x))/(f(x))) = Σ_(k=1) ^(2018) (1/(x+k)) ((f′(0))/(f(0))) = Σ_(k=1) ^(2018) (1/k) ((f′(0))/(2018!)) = H_(2018) f′(0) = 2018!×H_(2018)

$$\mathrm{I}\:\mathrm{suppose}\:\mathrm{you}\:\mathrm{mean} \\ $$$${f}\left({x}\right)\:=\:\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)…\left({x}+\mathrm{2018}\right) \\ $$$${f}\left({x}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{2018}} {\prod}}\left({x}+{k}\right) \\ $$$$\mathrm{ln}{f}\left({x}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{2018}} {\sum}}\mathrm{ln}\left({x}+{k}\right) \\ $$$$\frac{{f}'\left({x}\right)}{{f}\left({x}\right)}\:=\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{2018}} {\sum}}\frac{\mathrm{1}}{{x}+{k}} \\ $$$$\frac{{f}'\left(\mathrm{0}\right)}{{f}\left(\mathrm{0}\right)}\:=\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{2018}} {\sum}}\frac{\mathrm{1}}{{k}} \\ $$$$\frac{{f}'\left(\mathrm{0}\right)}{\mathrm{2018}!}\:=\:{H}_{\mathrm{2018}} \\ $$$${f}'\left(\mathrm{0}\right)\:=\:\mathrm{2018}!×{H}_{\mathrm{2018}} \\ $$

Facebook Tweet Pin

f-x-1-x-2-x-2018-f-0-

Leave a Reply Cancel reply