Question Number 166294 by cortano1 last updated on 18/Feb/22
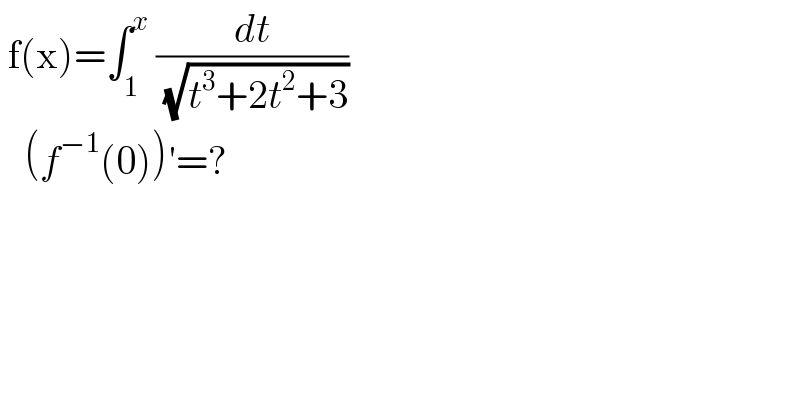
$$\:\mathrm{f}\left(\mathrm{x}\right)=\int_{\mathrm{1}} ^{{x}} \:\frac{{dt}}{\:\sqrt{{t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{2}} +\mathrm{3}}} \\ $$$$\:\:\:\left({f}^{−\mathrm{1}} \left(\mathrm{0}\right)\right)'=? \\ $$
Commented by cortano1 last updated on 18/Feb/22

$$\:\mathrm{not}\:\sqrt{\mathrm{6}}\:? \\ $$
Commented by mr W last updated on 18/Feb/22
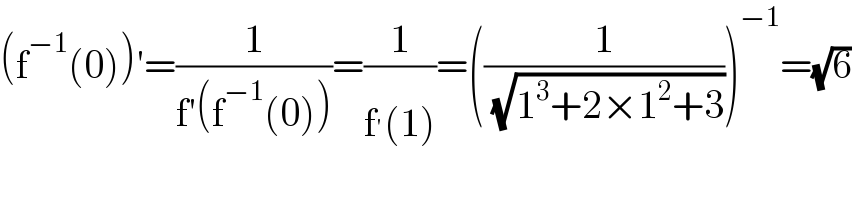
$$\left(\mathrm{f}^{−\mathrm{1}} \left(\mathrm{0}\right)\right)'=\frac{\mathrm{1}}{\mathrm{f}'\left(\mathrm{f}^{−\mathrm{1}} \left(\mathrm{0}\right)\right)}=\frac{\mathrm{1}}{\mathrm{f}^{'} \left(\mathrm{1}\right)}=\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}^{\mathrm{3}} +\mathrm{2}×\mathrm{1}^{\mathrm{2}} +\mathrm{3}}}\right)^{−\mathrm{1}} =\sqrt{\mathrm{6}} \\ $$
Commented by mr W last updated on 18/Feb/22

$${yes},\:\sqrt{\mathrm{6}}\:{is}\:{right}. \\ $$
Commented by mr W last updated on 18/Feb/22
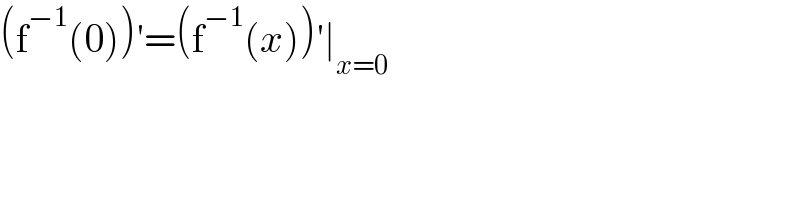
$$\left(\mathrm{f}^{−\mathrm{1}} \left(\mathrm{0}\right)\right)'=\left(\mathrm{f}^{−\mathrm{1}} \left({x}\right)\right)'\mid_{{x}=\mathrm{0}} \\ $$
Commented by mr W last updated on 18/Feb/22

$${see}\:{Q}\mathrm{166331} \\ $$
