Menu Close

f-x-1-x-x-5-1-x-5-f-3-

Tinku Tara 0 Comments
Pin




Question Number 181447 by Socracious last updated on 25/Nov/22
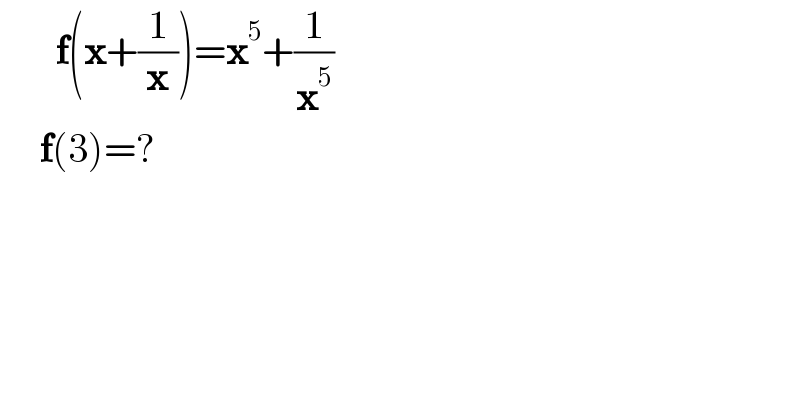
f(x+(1/x))=x^5 +(1/x^5 ) f(3)=?
$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}\right)=\boldsymbol{\mathrm{x}}^{\mathrm{5}} +\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}^{\mathrm{5}} } \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{f}}\left(\mathrm{3}\right)=? \\ $$
Answered by Frix last updated on 25/Nov/22
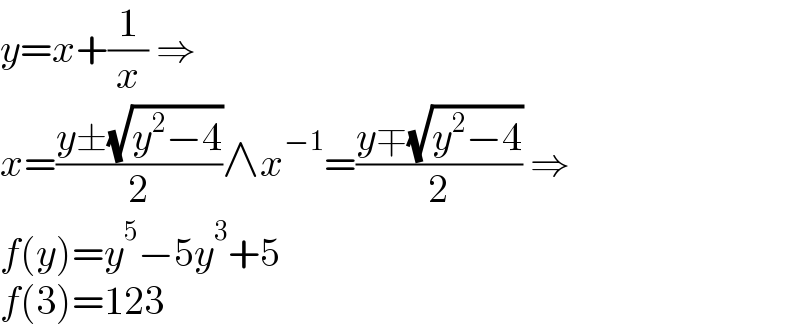
y=x+(1/x) ⇒ x=((y±(√(y^2 −4)))/2)∧x^(−1) =((y∓(√(y^2 −4)))/2) ⇒ f(y)=y^5 −5y^3 +5 f(3)=123
$${y}={x}+\frac{\mathrm{1}}{{x}}\:\Rightarrow \\ $$$${x}=\frac{{y}\pm\sqrt{{y}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\wedge{x}^{−\mathrm{1}} =\frac{{y}\mp\sqrt{{y}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\:\Rightarrow \\ $$$${f}\left({y}\right)={y}^{\mathrm{5}} −\mathrm{5}{y}^{\mathrm{3}} +\mathrm{5} \\ $$$${f}\left(\mathrm{3}\right)=\mathrm{123} \\ $$
Answered by manxsol last updated on 25/Nov/22
Answered by Rasheed.Sindhi last updated on 25/Nov/22
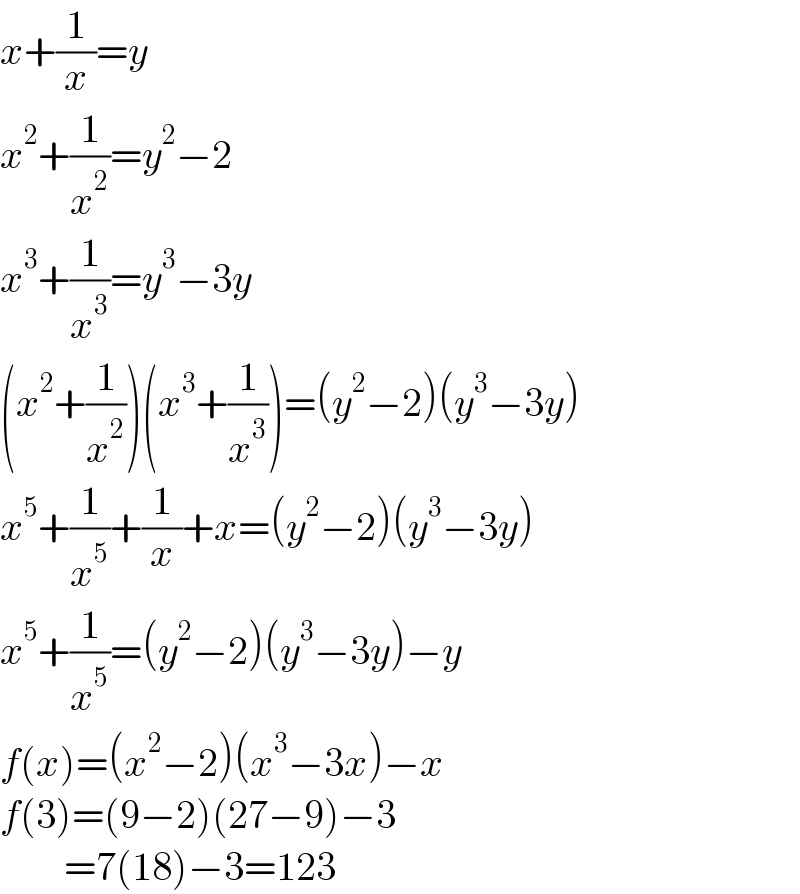
x+(1/x)=y x^2 +(1/x^2 )=y^2 −2 x^3 +(1/x^3 )=y^3 −3y (x^2 +(1/x^2 ))(x^3 +(1/x^3 ))=(y^2 −2)(y^3 −3y) x^5 +(1/x^5 )+(1/x)+x=(y^2 −2)(y^3 −3y) x^5 +(1/x^5 )=(y^2 −2)(y^3 −3y)−y f(x)=(x^2 −2)(x^3 −3x)−x f(3)=(9−2)(27−9)−3 =7(18)−3=123
$${x}+\frac{\mathrm{1}}{{x}}={y} \\ $$$${x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }={y}^{\mathrm{2}} −\mathrm{2} \\ $$$${x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }={y}^{\mathrm{3}} −\mathrm{3}{y} \\ $$$$\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\left({x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)=\left({y}^{\mathrm{2}} −\mathrm{2}\right)\left({y}^{\mathrm{3}} −\mathrm{3}{y}\right) \\ $$$${x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }+\frac{\mathrm{1}}{{x}}+{x}=\left({y}^{\mathrm{2}} −\mathrm{2}\right)\left({y}^{\mathrm{3}} −\mathrm{3}{y}\right) \\ $$$${x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }=\left({y}^{\mathrm{2}} −\mathrm{2}\right)\left({y}^{\mathrm{3}} −\mathrm{3}{y}\right)−{y} \\ $$$${f}\left({x}\right)=\left({x}^{\mathrm{2}} −\mathrm{2}\right)\left({x}^{\mathrm{3}} −\mathrm{3}{x}\right)−{x} \\ $$$${f}\left(\mathrm{3}\right)=\left(\mathrm{9}−\mathrm{2}\right)\left(\mathrm{27}−\mathrm{9}\right)−\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{7}\left(\mathrm{18}\right)−\mathrm{3}=\mathrm{123} \\ $$
Answered by Rasheed.Sindhi last updated on 25/Nov/22
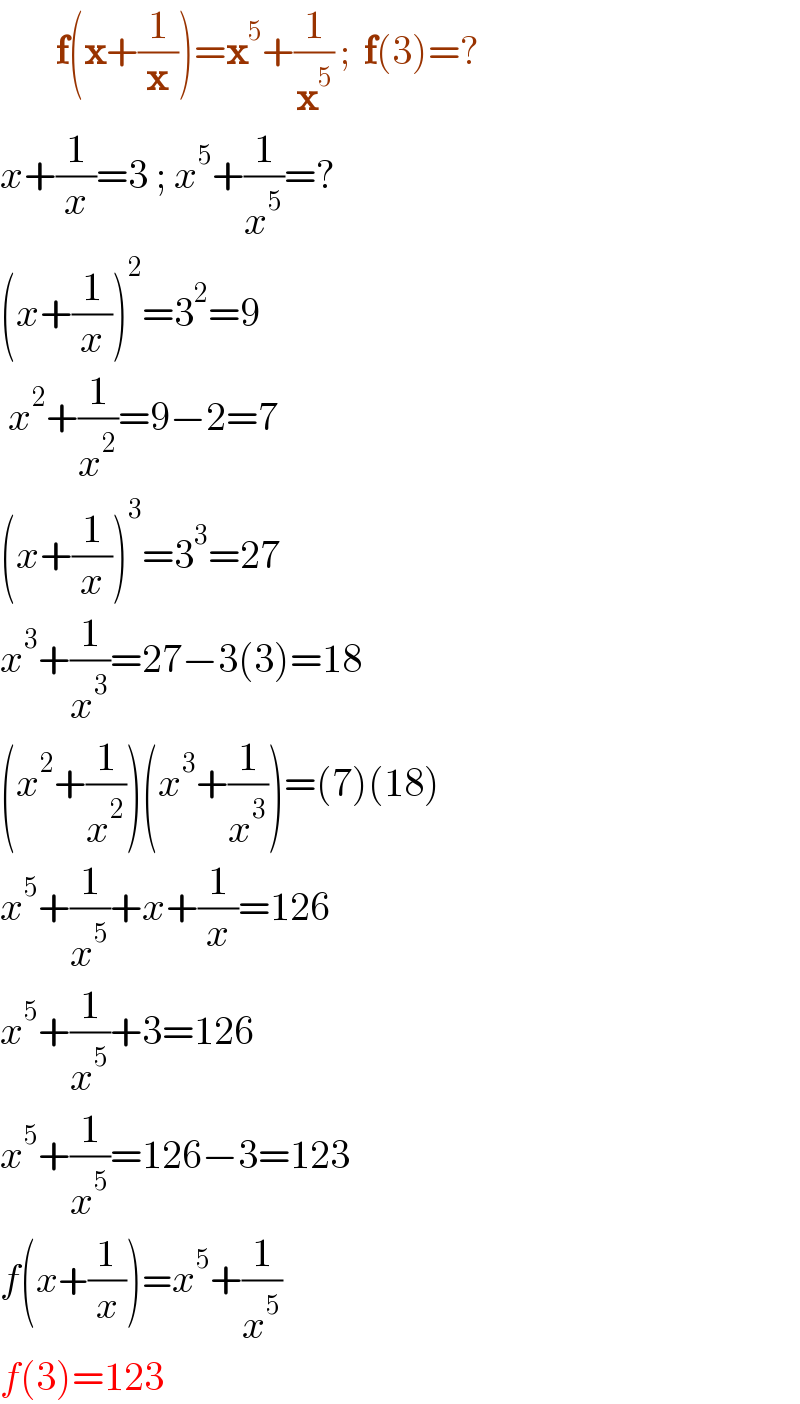
f(x+(1/x))=x^5 +(1/x^5 ) ; f(3)=? x+(1/x)=3 ; x^5 +(1/x^5 )=? (x+(1/x))^2 =3^2 =9 x^2 +(1/x^2 )=9−2=7 (x+(1/x))^3 =3^3 =27 x^3 +(1/x^3 )=27−3(3)=18 (x^2 +(1/x^2 ))(x^3 +(1/x^3 ))=(7)(18) x^5 +(1/x^5 )+x+(1/x)=126 x^5 +(1/x^5 )+3=126 x^5 +(1/x^5 )=126−3=123 f(x+(1/x))=x^5 +(1/x^5 ) f(3)=123
$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}\right)=\boldsymbol{\mathrm{x}}^{\mathrm{5}} +\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}^{\mathrm{5}} }\:;\:\:\boldsymbol{\mathrm{f}}\left(\mathrm{3}\right)=? \\ $$$${x}+\frac{\mathrm{1}}{{x}}=\mathrm{3}\:;\:{x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }=? \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} =\mathrm{3}^{\mathrm{2}} =\mathrm{9} \\ $$$$\:{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{9}−\mathrm{2}=\mathrm{7} \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{3}} =\mathrm{3}^{\mathrm{3}} =\mathrm{27} \\ $$$${x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }=\mathrm{27}−\mathrm{3}\left(\mathrm{3}\right)=\mathrm{18} \\ $$$$\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\left({x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)=\left(\mathrm{7}\right)\left(\mathrm{18}\right) \\ $$$${x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }+{x}+\frac{\mathrm{1}}{{x}}=\mathrm{126} \\ $$$${x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }+\mathrm{3}=\mathrm{126} \\ $$$${x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }=\mathrm{126}−\mathrm{3}=\mathrm{123} \\ $$$${f}\left({x}+\frac{\mathrm{1}}{{x}}\right)={x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} } \\ $$$${f}\left(\mathrm{3}\right)=\mathrm{123} \\ $$
Commented by manxsol last updated on 25/Nov/22
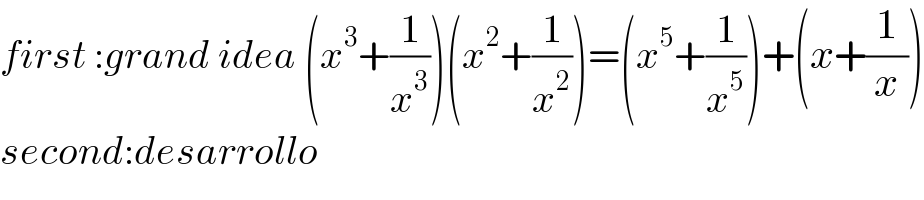
first :grand idea (x^3 +(1/x^3 ))(x^2 +(1/x^2 ))=(x^5 +(1/x^5 ))+(x+(1/x)) second:desarrollo
$${first}\::{grand}\:{idea}\:\left({x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)=\left({x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }\right)+\left({x}+\frac{\mathrm{1}}{{x}}\right) \\ $$$${second}:{desarrollo} \\ $$
Commented by Rasheed.Sindhi last updated on 26/Nov/22
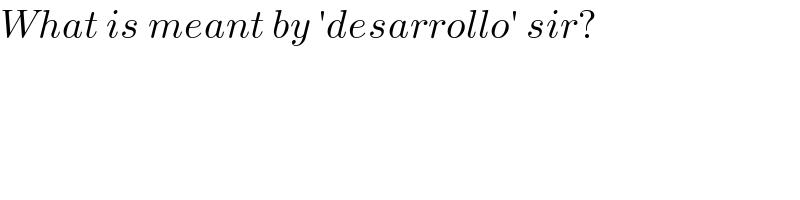
What is meant by ′desarrollo′ sir?
$${What}\:{is}\:{meant}\:{by}\:'{desarrollo}'\:{sir}? \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *